конічні перетину
конічні перетини
Конічні перетину - криві, що виходять при перетині кругового конуса (точніше - конічної поверхні) площиною, що не проходить через його вершину.
Отримувані при цьому обмежені фігури (рис. 1) виявляються еліпсами, а необмежені - гіперболами (якщо січна площина перетинає обидві порожнини конуса) або параболами (якщо січна площина перетинається лише з однією з його порожнин). Всі види конічних перетинів легко отримати за допомогою кишенькового ліхтарика, направляючи його під різними кутами на рівну площадку. Правда, при цьому у гіперболи ми побачимо лише одну гілку. Для того щоб побачити другу, потрібно вісь ліхтарика повернути на 180 °.

Однаковий спосіб отримання різних конічних перетинів тягне і схожість рівнянь, що описують ці криві. У січної площини можна так вибрати систему координат, щоб рівняння конічного перетину мало вигляд, де і - постійні. Якщо, то це рівняння визначає параболу при, еліпс - при, гіперболу - при. Геометричне властивість конічних перетинів, що міститься в наведеному рівнянні, було відомо давньогрецьким вченим і послужило для Аполлонія Пергського (приблизно II ст. До н.е.) приводом привласнити окремим типам конічних перетинів назви, що збереглися до наших днів: грецьке слово «парабола» означає « додаток »(так як в грецькій геометрії перетворення прямокутника даної площі в рівновеликий йому прямокутник з даною підставою називалося додатком даного прямокутника до цієї підстави); слово «еліпс» означає «недолік» (додаток з недоліком), слово «гіпербола» - «надлишок» (додаток з надлишком).

Дуже схожі рівняння конічних перетинів в полярних координатах. Якщо за полюс взяти фокус кривої, а за полярну вісь - вісь кривої, що проходить через фокус, то отримаємо рівняння
Воно буде рівнянням еліпса при (при одержимо окружність). Парабола буде описуватися цим рівнянням при, а гіпербола при. Число називається ексцентриситетом конічного перетину, а - його фокальним параметром.
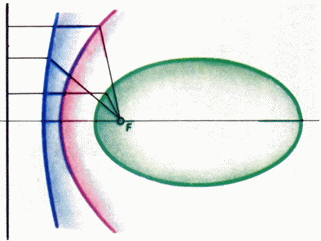
Математики Стародавньої Греції розглядали тільки перетину, перпендикулярні будь-якої утворює конуса, а різні типи кривих отримували шляхом зміни кута розчину конуса. Зокрема, вони виявили, що для будь-якого конічні перетини, крім кола, в його площині існує така пряма, для якої відношення відстаней точок на кривій до фокусу до відстані до цієї прямої дорівнює ексцентриситету цього конічного перетину (рис. 2). Така пряма була названа директоркою цієї кривої.
Математичний інтерес до конічних перетинах багато в чому обумовлений тим, що якщо записати рівняння такого перетину в довільній декартовій системі координат на січної площини, то воно завжди буде алгебраїчним рівнянням другого порядку, тобто матиме вигляд:
І навпаки, крива, описувана таким рівнянням, є конічним перетином, за винятком випадків, коли коефіцієнти цього рівняння пов'язані певними співвідношеннями.
Всі тіла Сонячної системи рухаються навколо Сонця по еліпсам. Небесні тіла, що потрапляють в Сонячну систему з інших зоряних систем, рухаються навколо Сонця по гіперболічної орбіті і, якщо на їх рух не роблять істотного впливу планети Сонячної системи, залишають се по цій же орбіті. За еліпсам рухаються навколо Землі її штучні супутники і природний супутник - Місяць, а космічні кораблі, запущені до інших планет, рухаються по закінченні роботи двигунів по парабола або гіпербол (в залежності від швидкості) до тих пір, поки тяжіння інших планет або Сонця не стане порівняно з земним тяжінням (рис. 3).
