Кінетична і потенційна енергія (2)
Кінетична енергія - енергія механічної системи, що залежить від швидкостей руху її точок. Часто виділяють кінетичну енергію поступального і обертального руху. Одиниця виміру в системі СІ - Джоуль. Більш строго, кінетична енергія є різниця між повною енергією системи і її енергією спокою; таким чином, кінетична енергія - частина повної енергії, обумовлена рухом.
Розглянемо випадок, коли на тіло масою m діє постійна сила (вона може бути рівнодіюча кількох сил) і вектори сили і переміщення спрямовані вздовж однієї прямої в одну сторону. У цьому випадку роботу сили можна визначити як A = F ∙ s. Модуль сили по другим законом Ньютона дорівнює F = m ∙ a, а модуль переміщення s при рівноприскореному прямолінійному русі пов'язаний з модулями початковій υ1 і кінцевої υ2 швидкості і прискорення а виразом
Звідси для роботи отримуємо
Фізична величина, що дорівнює половині твори маси тіла на квадрат його швидкості, називаетсякінетіческой енергією тіла.
Кінетична енергія позначається буквою Ek.
Тоді рівність (1) можна записати в такому вигляді:
Теорема про кінетичну енергію:
робота рівнодіючої сил, прикладених до тіла, дорівнює зміні кінетичної енергії тіла.
Так як зміна кінетичної енергії дорівнює роботі сили (3), кінетична енергія тіла виражається в тих же одиницях, що і робота, т. Е. В джоулях.
Якщо початкова швидкість руху тіла масою т дорівнює нулю і тіло збільшує свою швидкість до значення υ. то робота сили дорівнює кінцевому значенню кінетичної енергії тіла:
Фізичний смислкінетіческой енергії:
кінетична енергія тіла, що рухається зі швидкістю υ, показує, яку роботу повинна зробити сила, що діє на покоїться тіло, щоб повідомити йому цю швидкість.
Потенційна енергія - мінімальна робота, яку необхідно зробити, щоб перенести тіло з якоїсь точки відліку в дану точку в поле консервативних сил. Друге визначення: потенційна енергія - це функція координат, яка є складовою в лагранжіаном системи, і описує взаємодію елементів системи. Третє визначення: потенційна енергія - це енергія взаємодії. Одиниці виміру [Дж]
Потенційна енергія приймається рівною нулю для деякої точки простору, вибір якої визначається зручністю подальших обчислень. Процес вибору даної точки називається нормуванням потенційної енергії. Зрозуміло також, що коректне визначення потенційної енергії може бути дано тільки в поле сил, робота яких залежить тільки від початкового і кінцевого положення тіла, але не від траєкторії його переміщення. Такі сили називаються консервативними.
Потенційна енергія піднятого над Землею тіла - це енергія взаємодії тіла і Землі гравітаційними силами. Потенційна енергія пружно деформованого тіла - це енергія взаємодії окремих частин тіла між собою силами пружності.
Потенціальниміназиваютсясіли, робота яких залежить тільки від початкового і кінцевого положення рухається матеріальної точки або тіла і не залежить від форми траєкторії.
При замкнутій траєкторії робота потенційної сили завжди дорівнює нулю. До потенційних силам відносяться сили тяжіння, сили пружності, електростатичні сили і деякі інші.
Сили, робота яких залежить від форми траєкторії, називаютсянепотенціальнимі. При переміщенні матеріальної точки або тіла по замкнутій траєкторії робота непотенційного сили не дорівнює нулю.
Потенційна енергія взаємодії тіла з Землею.
Знайдемо роботу, що здійснюються силою тяжіння Fт при переміщенні тіла масою т вертикально вниз з висоти h1 над поверхнею Землі до висоти h2 (рис. 1).
Якщо різниця h1 - h2 дуже мала в порівнянні з відстанню до центру Землі, то силу тяжіння Fт під час руху тіла можна вважати постійною і рівною mg.
Так як переміщення збігається за напрямком з вектором сили тяжіння, робота сили тяжіння дорівнює
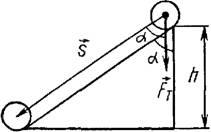
Розглянемо тепер рух тіла по похилій площині. При переміщенні тіла вниз по похилій площині (рис. 2) сила тяжіння Fт = m ∙ g здійснює роботу
де h - висота похилій площині, s - модуль переміщення, рівний довжині похилій площині.
Рух тіла з точки В в точку С по будь-якій траєкторії (рис. 3) можна подумки уявити що складається з переміщень по ділянках похилих площин з різними висотами h '. h "і т. д. Робота А сили тяжіння на всьому шляху з В в С дорівнює сумі робіт на окремих ділянках шляху:
де h1 і h2 - висоти від поверхні Землі, на яких розташовані відповідно точки В і С.
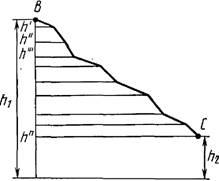
Рівність (7) показує, що робота сили тяжіння не залежить від траєкторії руху тіла і завжди дорівнює добутку модуля сили тяжіння на різницю висот в початковому і кінцевому положеннях.
При русі вниз робота сили тяжіння позитивна, при русі вгору - негативна. Робота сили тяжіння на замкнутої траєкторії дорівнює нулю.
Рівність (7) можна представити в такому вигляді:
Фізичну величину, що дорівнює добутку маси тіла на модуль прискорення вільного падіння і на висоту, на яку піднято тіло над поверхнею Землі, називаютпотенціальной енергіейвзаімодействія тіла і Землі.
Робота сили тяжіння при переміщенні тіла масою т з точки, розташованої на висоті h2, в точку, розташовану на висоті h1 від поверхні Землі, по будь-якій траєкторії дорівнює зміні потенційної енергії взаємодії тіла і Землі, взятому з протилежним знаком.
Потенційна енергія позначається буквою Ер.
Значення потенційної енергії тіла, піднятого над Землею, залежить від вибору нульового рівня, т. Е. Висоти, на якій потенційна енергія приймається рівною нулю. Зазвичай приймають, що потенційна енергія тіла на поверхні Землі дорівнює нулю.
При такому виборі нульового рівня потенційна енергія Ер тіла, що знаходиться на висоті h над поверхнею Землі, дорівнює добутку маси m тіла на модуль прискорення вільного падіння g і відстань h його від поверхні Землі:
Фізичний смислпотенціальной енергії взаємодії тіла з Землею:
потенційна енергія тіла, на яке діє сила тяжіння, дорівнює роботі, яку здійснюють силою тяжіння при переміщенні тіла на нульовий рівень.
На відміну від кінетичної енергії поступального руху, яка може мати лише позитивні значення, потенційна енергія тіла може бути як позитивною, так і негативною. Тіло масою m. що знаходиться на висоті h, де h