Кінетична і потенційна енергії - студопедія
Кінетична енергія механічної системи - це енергія механічного руху цієї системи.
Сила F. діючи на покоїться тіло і викликаючи його рух, здійснює рабо-ту, а енергія рухомого тіла віку-ет на величину витраченої роботи. Таким чином, робота dA сили F на шляху, кото-рий тіло пройшло за час зростання швидкості від 0 до v, йде на збільшення кінетичної енергії dT тіла, т. Е.
Використовуючи другий закон Ньютона F = mdv / dt
і примножуючи обидві частини дорівнює ства на переміщення dr. отримаємо
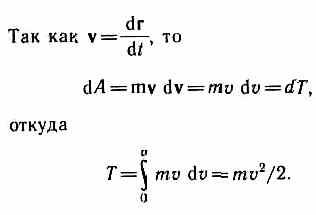
Таким чином, тіло масою т, що рухає-ся зі швидкістю v, має кінетичної енергією
З формули (12.1) видно, що кінетична енергія залежить тільки від маси і швидкості тіла, т. Е. Кінетична енергія системи є функція стану її дві-вання.
При виведенні формули (12.1) предпола-галось, що рух розглядається в інерціальній системі відліку, так як інакше можна було б використовувати за-кони Ньютона. У різних інерційних системах відліку, що рухаються один відно-сительно одного, швидкість тіла, а слідові-тельно, і його кінетична енергія будуть неоднакові. Таким чином, кинетич-ська енергія залежить від вибору системи відліку.
Потенційна енергія - механічного-ська енергія системи тіл, що визначається їх взаємним розташуванням і характе-ром сил взаємодії між ними.
Нехай взаємодія тел осуществля-ється за допомогою силових полів (напри-заходів, поля пружних сил, поля гравітаційних-них сил), що характеризуються тим, що робота, що здійснюються діючими сила-ми при переміщенні тіла з одного поло-ження в інше, не залежить від того, по якій траєкторії це переміщення виро-зошло, а залежить тільки від початкового і кінцевого положень. Такі поля на-ни опиняються потенційними, а сили, дей-ціалу в них, - консервативними. Якщо ж робота, що здійснюються силою, залежить від траєкторії переміщення тіла з однієї точки в іншу, то така сила називається дисипативної; її прикладом є сі-ла тертя.
Тіло, перебуваючи в потенційному полі сил, має потенційну енергією II. Робота консервативних сил при елементів-тарному (нескінченно малому) зміні конфігурації системи дорівнює приросту потенційної енергії, взятому зі знаком мінус, так як робота виконується за рахунок зменшення потенційної енергії:
Робота dА виражається як скалярний твір сили F на переміщення dr і вираз (12.2) можна записати у вигляді
Отже, якщо відома функція П (r), то з формули (12.3) можна знайти силу F по модулю і напрямку.
Потенційна енергія може бути визначена виходячи з (12.3) як
де С - постійна інтегрування, т. е. потенційна енергія визначається з точністю до деякої довільної по-постійної. Це, однак, не позначається на фізичних законах, так як в них входить або різниця потенційних енергій в двох положеннях тіла, або похідна П за координатами. Тому потенціалом-ву енергію тіла в якомусь визначено-ном положенні вважають рівною нулю (ви-відбирають нульовий рівень відліку), а енергію тіла в інших положеннях відраховуючи-ють щодо нульового рівня. Для консервативних сил
або у векторному вигляді
(I, j, k - одиничні вектори координат-них осей). Вектор, який визначається висловлю-ням (12.5), називається градієнтом ска-ляра П.
Для нього поряд з позначенням grad П застосовується також позначення ÑП. Ñ ( «Набла») означає символічний вектор, називає-мий оператором Гамільтона або Набла-оператором:
Конкретний вид функції П залежить від характеру силового поля. Наприклад, по-потенційного енергія тіла масою т, під-нятого на висоту h над поверхнею Зем-ли, дорівнює
де висота h відраховується від нульового рівня, для якого П0 = 0. Вираз (12.7) випливає безпосередньо з того, що потенційна енергія дорівнює роботі сили тяжіння при падінні тіла з висоти h на поверхню Землі.
Так як початок відліку вибирається довільно, то потенційна енергія може мати від'ємне значення (ки-генетичних енергія завжди позитивними-на! ». Якщо прийняти за нуль потенційну енергію тіла, що лежить на поверхні Землі, то потенційна енергія тіла, що знаходиться на дні шахти (глибина h '), П = -mgh'.
Знайдемо потенційну енергію упругодеформірованному тіла (пружини). Сила пружності пропорційна дефор-мації:
де Fxупр - проекція сили пружності на вісь х; k - коефіцієнт пружності (для пружини - жорсткість), а знак мінус вка-показують, що Fxупр спрямована в бік, протилежний деформації х.
За третім законом Ньютона, дефор-мірующая сила дорівнює по модулю силі пружності і протилежно їй направле-на, т. Е.
Fx = -Fxупр = kx Елементарна робота dA, що здійснюються силою Fx при нескінченно малій деформації dx, дорівнює
а повна робота
йде на збільшення потенційної енергії пружини. Таким чином, потенційна енергія упругодеформірованному тіла
Потенційна енергія системи, під-бно кінетичної енергії, є функ-цією стану системи. Вона залежить толь-ко від конфігурації системи та її положе-ня по відношенню до зовнішніх тіл.
Повна механічна енергія систе-ми - енергія механічного руху і взаємодії:
т. е. дорівнює сумі кінетичної і потен-них енергій.