Як побудувати фрактал безліч аполлона

Частина 2 з 2: Побудова безлічі Аполлона Правити

Безліч Аполлона приймає форму красивою фрактальної конструкції з скорочуються в розмірі кіл. Математично безліч Аполлона нескінченно складне, але чи використовуєте ви комп'ютерну програму, або традиційні інструменти для малювання, ви в кінцевому підсумку досягнете того моменту, коли буде неможливо намалювати коло меншого розміру. Зауважте, що чим точніше ви малюєте окружності, тим більше вони будуть відповідати безлічі Аполлона.

Почніть з одного великого кола. Ваша перша задача - просто намалювати одну велику, ідеально рівну окружність. Чим більше коло, тим складніше може бути ваш фрактал, тому намагайтеся побудувати таку окружність, яку дозволяє розмір паперу, або так, щоб можна було її повністю бачити на екрані в графічній програмі.

Намалюйте коло поменше в першій окружності, яка буде стосуватися її в одній точці. Отже, накресліть коло всередині нашої першої окружності, вона буде менше, ніж основна, але все одно досить велика. Точний розмір другої окружності залежить від вас, так як немає встановленого розміру. Однак, давайте накреслив другу окружність так, щоб вона займала половину основного кола. Іншими словами, її центр - це середина радіусу більшої окружності.

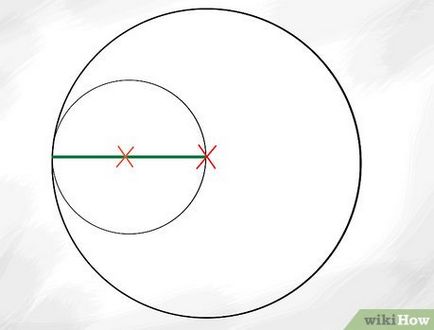
• Запам'ятайте, що в безлічі Аполлона все окружності є дотичними один до одного. Якщо ви користуєтеся циркулем при побудові кіл, відтворити цей ефект, поставивши гострий кінець циркуля посередині радіуса основного кола, і відрегулювати олівець циркуля таким чином, щоб він просто торкався краю кола, і потім намалюйте меншу внутрішню окружність.

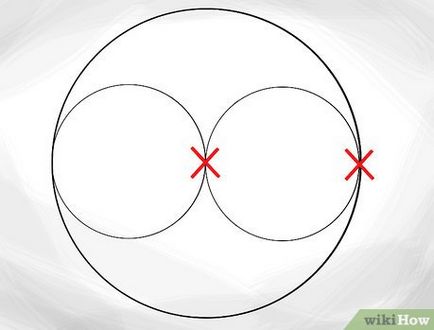
Накресліть ідентичну окружність поруч з меншою внутрішньою окружністю. Отже, давайте намалюємо іншу окружність поруч з першою. Окружність повинна бути дотичній до обох колах: зовнішньої більшою і внутрішньої меншою, що означає, що обидві внутрішніх окружності стикнутися точно в центрі великий.

Застосуйте теорему Декарта, щоб обчислити розміри таких кіл. На мить перестанемо малювати. Тепер, коли у нас є три кола під фрактале, ми можемо використовувати теорему Декарта, щоб знайти радіус наступної окружності, яку будемо малювати. Запам'ятайте рівняння теореми Декарта d = a + b + c ± 2 (√ (a × b + b × c + c × a)). де a, b, і c є кривизною трьох дотичних кіл і d - кривизна кола дотичній до всіх трьох. Тому, щоб знайти радіус нашого наступного кола, давайте розрахуємо кривизну кожної наявної у нас окружності, поки не зможемо знайти кривизну наступної окружності і потім розрахуємо її радіус.

• Давайте визначимо радіус зовнішнього кола як 1. Так як інші кола знаходяться всередині неї, ми маємо справу з «внутрішньої» кривизною (замість зовнішньої), і, отже, ми знаємо, що вона негативна. - 1 / r = -1/1 = -1. Так кривизна великому колу дорівнює -1.
• Радіус менших кіл становить половину радіуса великий, тобто 1/2. Так як ці кола стикаються один з одним і основний окружністю зовнішніми сторонами, ми маємо справу із зовнішньою кривизною, позитивною. 1 / (1/2) = 2. Тому кривизна менших кіл дорівнює 2.
• Тепер ми знаємо, що a = -1, b = 2, і c = 2 в нашому рівнянні теореми Декарта. Давайте обчислимо d:
  • d = a + b + c ± 2 (√ (a × b + b × c + c × a))
  • d = -1 + 2 + 2 ± 2 (√ (-1 × 2 + 2 × 2 + 2 × -1))
  • d = -1 + 2 + 2 ± 2 (√ (-2 + 4 + -2))
  • d = -1 + 2 + 2 ± 0
  • d = -1 + 2 + 2
  • d = 3. Кривизна наступної окружності 3. Так як 3 = 1 / r, радіус цієї окружності буде дорівнює 1/3.

Накресліть наступну пару кіл. Щоб намалювати такі дві окружності, використовуйте значення радіусу, які ви тільки що знайшли. Не забувайте, що ці кола є дотичними до тих, чия кривизна була використана при підрахунку теореми Декарта. Іншими словами, вони будуть стосуватися і основний і вторинних кіл. Щоб ці кола стосувалися трьох інших, вам потрібно накреслити їх у вільній області зверху і знизу в основному колі.

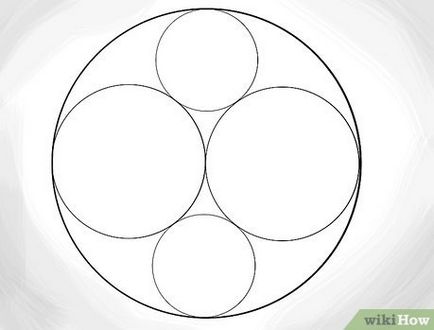
• Пам'ятайте, що радіус цих кіл дорівнює 1/3. Відміряйте 1/3 від краю зовнішньої окружності і потім накресліть нову. Вона повинна бути дотичній до всіх трьох довколишніх колах.

Таким чином продовжуйте додавати окружності. Так як вони є фракталами, безліч Аполлона нескінченно складне. Це означає, що ви можете додавати окружності все меншого і меншого розміру до основи фрактала. Ви обмежені лише точністю ваших інструментів (або, якщо ви використовуєте комп'ютер, здатністю графічної програми до збільшення). Кожна окружність, якою б маленькою вона не була, повинна бути дотичній до трьох інших. Щоб намалювати кожну наступну окружність, використовуйте значення кривизни трьох дотичних до неї кіл для теореми Декарта. Потім за допомогою відповіді точно накресліть нову окружність.

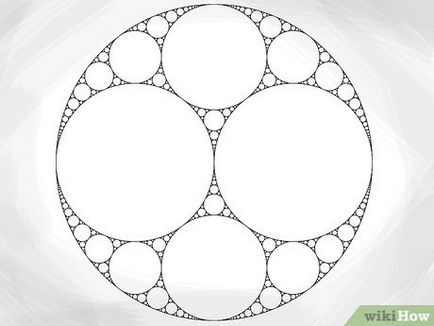
• Зверніть увагу, що безліч, яке ми вибрали для побудови, симетрично, тому радіус одному колі такий же, як радіус ідентичною їй окружності. Однак, не всі безлічі Аполлона симетричні.
• Давайте розберемо ще один приклад. Припустимо, після побудови останньої пари кіл, ми захочемо накреслити кола, дотичні до нашої третій парі і основного кола. Кривизна цих кіл дорівнює 3, 2 і -1 відповідно. Тепер включаємо ці числа в теорему Декарта, встановивши, що a = -1, b = 2, і c = 3:
  • d = a + b + c ± 2 (√ (a × b + b × c + c × a))
  • d = -1 + 2 + 3 ± 2 (√ (-1 × 2 + 2 × 3 + 3 × -1))
  • d = -1 + 2 + 3 ± 2 (√ (-2 + 6 + -3))
  • d = -1 + 2 + 3 ± 2 (√ (1))
  • d = 2, 6. У нас дві відповіді! Однак, ми знаємо, що наша нова окружність буде менше, ніж дотичні до неї, значить мати сенс буде тільки значення кривизни 6 (а радіус 1/6).
  • Інший відповідь, 2, насправді відноситься до гіпотетичної окружності на «іншій стороні» точки дотичній до другої і третьої окружності. Ця окружність є дотичній до обох цих кіл і до основної, але вона буде перетинати ті кола, які ми вже намалювали, тому можна проігнорувати цю відповідь.

Як випробування, постарайтеся побудувати несиметричне безліч Аполлона, змінюючи розмір другої окружності. Всі безлічі Аполлона починають будувати з одного і того ж - з великою зовнішньою окружності, яка і є кордоном фрактала. Однак, немає необхідності в тому, щоб радіус другий окружності дорівнював 1/2 першої. Ми просто вирішили взяти ці числа для простоти і легкості в розумінні. Для задоволення спробуйте побудувати нове безліч з другої окружністю іншого розміру - це призведе до нових напрямків в дослідженні.

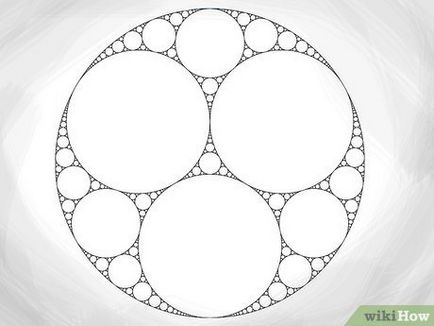
• Після того як побудуєте другу окружність (незалежно від її розміру), вашим наступним дією має бути побудова однієї (або більше) окружності, яка є дотичною і до другої, і до основної зовнішньої колах - немає єдино вірного способу, як її побудувати. Після цього ви можете скористатися теоремою Декарта для визначення радіуса наступних кіл, як показано вище.