Хвилі в пружних середовищах
Уявімо собі на поверхні води хвилю у вигляді одиничного горба або солітон, рис. 9, що поширюється в певному напрямку. За методом Фур'є таке складність -
ве коливання може бути розкладено на групу чисто гармонійних коливань. Якщо все гармонійні коливання поширюються по поверхні води з однаковими скорос -
тями, то з тією ж швидкістю буде поширюватися і утворене ними складне колеба -
ня. Але, якщо швидкості окремих косинусоидальной хвиль різні, то безперервно змінюються різниці фаз між ними, і горб, що виникає в результаті їх складання, безперервно змінює свою форму і переміщається зі швидкістю, яка не співпадає з фазовою швидкістю жодної з доданків хвиль.
Всякий відрізок косинусоид, рис. 10, теж може по теоремі Фур'є розкладений на безліч необмежених у часі ідеальних косинусоид. Таким чином, будь-яка реальна хвиля являє собою накладення # 150; групу # 150; нескінченних косинусоид, і швидкість її поширення в диспергуючих середовищі відмінна від фазової швидкості доданків хвиль. Ця швидкість поширення реальних хвиль в диспергуюча -
щей середовищі і носить назву групової швидкості. Тільки в середовищі, позбавленої дисперсії, реальна хвиля поширюється зі швидкістю, що збігається з фазовою швидкістю тих косинусоидальной хвиль, складанням яких вона утворена.
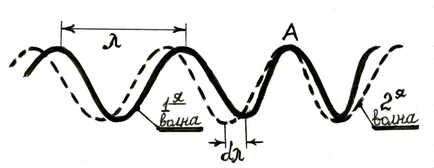

До висновку вирази для групової швидкості
Припустимо, що група хвиль складається з двох хвиль, мало різняться по довжині:
a) хвилі з довжиною хвилі. поширюються зі швидкістю;
b) хвилі з довжиною хвилі. поширюються зі швидкістю
Відносне розташування обох хвиль для деякого моменту часу представлено на рис. 11. a. Горби обох хвиль сходяться в точці; в одному місці розташований максимум результуючих коливань. Нехай. тоді друга хвиля обганяє першу. Через деякий проміжок часу вона обжене її на відрізок; в результаті чого горби обох хвиль будуть вже складатися в точці. Мал. 11. b. т. е. місце максимуму результуючого складного коливання виявиться зміщеним назад на відрізок, рівний. Звідси швидкість поширення максимуму результуючих коливань щодо середовища виявиться менше швидкості поширення першої хвилі на величину. Ця швидкість поширення максимуму складного коливання і є групова швидкість; позначаючи її через, маємо
Так як швидкість другої хвилі щодо першої дорівнює. то
підставимо тепер (37) в останню формулу і отримаємо
Застосуємо цей вислів для в (38) знайдемо для групової швидкості
З (39) видно, що групова швидкість тим більше відрізняється від фазової швидкості. чим більше. т. е. чим сильніше виражена залежність швидкості поширення хвиль від їх довжини, звана дисперсією.
При групова швидкість. а при маємо. Отже групова швидкість може бути як менше, так і більше фазової швидкості.
Групова швидкість менше фазової, коли. т. е. коли довші хвилі поширюються швидше коротших; цей випадок носить назву нормальної дисперсії;
Для середовища позбавленої дисперсії і. т. е. групова і фазова швидкості збігаються.
Якщо. то короткі по довжині хвилі обганяють довші; цей випадок носить назву аномальної дисперсії.
- Принцип суперпозиції хвиль
При поширенні в середовищі кількох хвиль малої амплітуди виконуючи -
ється, відкритий Леонардо да # 150; Вінчі, принцип суперпозиції: коливання кожної частинки середовища визначається як сума незалежних коливань, які здійснювали б ці частинки при поширенні кожної хвилі окремо. Принцип суперпозиції порушується тільки для хвиль з дуже великою амплітудою, наприклад, в нелінійній оптиці. Хвилі, що характеризуються однаковою частотою і постійної, що не залежить від часу, різницею фаз, називають когерентними; наприклад, наприклад, косінусоідаль -
ні або синусоїдальні хвилі з однаковою частотою.
Інтерференцією називають складання когерентних хвиль, в результаті якого виникає стійке в часі посилення коливань в одних точках і ослаблення його в інших. При цьому відбувається перерозподіл енергії коливань між сусідніми областями середовища. Інтерференція хвиль відбувається тільки, якщо вони когерентні.
Особливим прикладом результату інтерференції двох хвиль служать так
звані стоячі хвилі, які утворюються в результаті накладання двох зустрічних плоских хвиль з однаковими амплітудами.
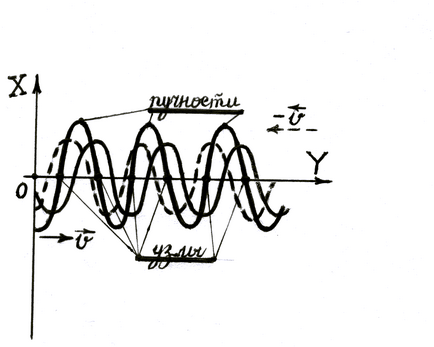
Додавання двох хвиль, що поширюються в протилежних напрямках
Припустимо, що дві плоскі хвилі з однаковими амплітудами распростра -
няются # 150; одна з позитивного спрямо -
тичних. Мал. 12, інша # 150; по отрица -
Якщо початок координат взяти в такий точ -
ке, в якій зустрічні хвилі мають однакові напрямки зміщення, т. е. мають однакові фази, і вибрати відлік часу так, щоб початкові фази ока -
залісь рівними нулю, то рівняння каж -
дою плоскої хвилі можна написати у вигляді:
a) для хвилі (8), що йде в бік поло -
a) для хвилі (8), що йде в бік позитивної осі
b) для хвилі (9), що розповсюджується в бік негативного напрямку.
де - амплітуда гармонійної хвилі або амплітуда коливань в цій хвилі.
Додавання цих двох хвиль дає
звідки, розкриваючи значення косинусів від складних аргументів і виробляючи скорочення, маємо
В (40) множник показує, що в точках середовища виникає коливання з тієї ж частотою. що і коливання зустрічних хвиль.
Множник. що не залежить від часу, висловлює амплітуду
результуючого коливання; точніше # 150; амплітуда, як величина істотно позитивна за своїм визначенням, дорівнює абсолютному значенню цього множника:
Таким чином, амплітуда коливання залежить від координати. визначає положення точок середовища.
Що виникає сумнів (40) носить назву стоячій хвилі.
У певних точках амплітуда стоячої хвилі дорівнює сумі амплітуд обох доданків, такі точки називаються пучностями;
в інших точках результуюча амплітуда дорівнює нулю, ці точки називаються вузлами стоячої хвилі.
Амплітуда, що визначається (41), максимальна в точках, для яких
Звідси положення пучностей визначиться умовою
Отже, координати пучностей рівні
Відстань між сусідніми пучностями отримаємо, використовуючи (42)
т. е. відстань між двома сусідніми пучностями дорівнює половині довжини тих хвиль, в результаті інтерференції яких утворюється дана стояча хвиля.
У вузлах амплітуда результуючого коливання дорівнює нулю, звідси по (41) умова освіти вузлів:
отже, координати вузлів рівні
і значить, що відстань вузла від найближчої пучности одно
т. е. вузли та пучности відстоять один від одного на чверть довжини хвилі.
Так як в даний момент часу множник має для всіх точок однакове значення, то всі крапки між двома вузлами коливаються в однакових фазах, т. Е. Вони одночасно досягають максимальних відхилень, одночасно проходять через положення рівноваги і т. Д. Точки, що лежать по обидві боку одного і того ж вузла, коливаються в протилежних фазах, т. е. досягають одночасно крайніх, але протилежних за знаком зсувів, проходять одночасно положення рівноваги, але з протилежно спрямованими швидкостями і т. д.
Аверроїзм - філософсько-теологічний напрямок в західно-європейської філософії епохи середньовіччя і Відродження, що виходив з поглядів араб. філософа Аверроеса (Ібн Рушда). Аверроїзм розробляв матеріалістичні тенденції арістотелізма- ідею вічності (отже, нестворене) світу.