Ханойська вежа - problem solving with algorithms and data structures
Головоломка про Ханойські вежі була винайдена французьким математиком Едуардом Лукасом в 1883 році. Його надихнула легенда, яка розповідає про замок Хинду, де це завдання поставили перед юними жерцями. На початку часів їм дали три стержня і стопку з шістдесяти чотирьох золотих дисків, кожен з яких трохи менше попереднього. Було потрібно переставити все диски з одного стрижня на інший, дотримуючись два строгих умови. По-перше, за раз можна було переміщати тільки один диск. По-друге, не можна класти більший диск поверх меншого. Жерці працювали (і працюють донині) дуже швидко, день і ніч, переставляючи кожну секунду по одному диску. Легенда свідчить, що коли вони закінчать свою роботу, замок звернеться в пил, і світ зникне.
Хоча легенда і цікава, вам не варто турбуватися про швидкий кінець світу. Число ходів, потрібних для правильної перестановки вежі з 64 дисків, дорівнює \ (2 ^ -1 = 18,446,744,073,709,551,615 \). Зі швидкістю один хід в секунду це займе \ (584,942,417,355 \) років! Велика цифра для такої нескладної на перший погляд головоломки.
Малюнок 1 показує приклад конфігурації дисків в середині переміщення з першого кілочка на третій. Зверніть увагу, що (як регламентовано правилами) диски на кожному з кілочків складаються таким чином, щоб менший завжди лежав на більшій. Якщо ви ніколи раніше не намагалися вирішити цю головоломку, то можете спробувати зараз. Для це не потрібні справжні диски і стрижні - спрацює і стопка книг або аркушів паперу.
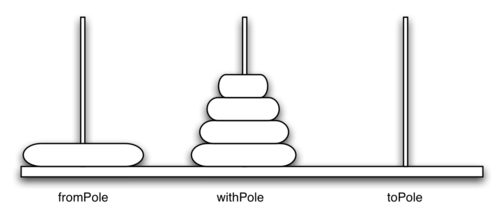
Малюнок 1: Приклад розташування дисків Ханойська вежі.
Як нам вирішити це завдання рекурсивно? З чого б ви почали? Що є тут базовим випадком? Давайте подумаємо над цим від кінця до початку. Припустимо, спочатку на першому кілочку у вас знаходиться вежа з п'яти дисків. Якщо ви вже знаєте, як пересунути чотири з них на другий кілочок, то можете з легкістю перекласти нижній диск на стрижень №3, а потім перекласти туди ж вежу зі стрижня №2. Але що, якщо ви поняття не маєте, як перемістити вежу з чотирьох верхніх? Припустимо, що відомо, як пересунути вежу з трьох верхніх дисків на третій кілочок. Тоді з переміщенням четвертого труднощів не виникне: перекладіть його на другий стрижень, а потім покладіть зверху ті, що нанизані на третій. Але якщо ви не знаєте як перемістити три? Що ж, можна перекласти вежу з двох дисків на стрижень №2, а третій - на стрижень №3, а потім зверху покласти вежу з двох. Але якщо до цих пір не зрозуміло, як це зробити? Упевнений, що ви погодитеся: перемістити один диск на третій кілочок легше легкого - тривіальніше нічого не знайдеться. Звучить як базовий випадок, а?
Ось загальна схема того, як перемістити вежу з вихідного стрижня на заданий з використанням проміжного:
- Пересунути вежу з (кількість дисків - 1) на проміжний кілочок, використовуючи при цьому заданий.
- Покласти залишився диск на заданий стрижень.
- Перемістити вежу з решти на проміжному стрижні дисків на кінцевий, використовуючи при цьому початковий кілочок.
Поки ми слідуємо правилом, що більший диск знаходиться внизу стека, можна використовувати три описаних кроку рекурсивно, обробляючи будь-які більші диски, як ніби їх там і не було. Єдина річ, яку ми втратили в схемі вище, - це ідентифікація базового випадку. Найпростіша ханойська вежа - це вежа з одного диска. У цьому випадку нам потрібно всього лише пересунути єдиний диск на його кінцеве місце призначення. Вежа з одного диска стане нашим базовим випадком. До речі, кроки схеми вище ведуть до нього, зменшуючи кожен раз висоту вежі на одиницю в пунктах 1 і 3. Лістинг 1 показує код на Python для вирішення завдання про Ханойські вежі.
Зауважте, що лістинг 1 практично ідентичний словесному опису. Ключ до простоти алгоритму в тому, що ми робимо два різних рекурсивних виклику: один в рядку 3, а другий - в рядку 5. У рядку 3 ми переміщаємо все диски, крім нижнього, з початкового стержня на проміжний. Наступний рядок просто переставляє нижній диск на його кінцеву позицію. Потім в рядку 5 ми переміщаємо вежу з проміжного стрижня поверх найбільшого диска. Базовий випадок виявляється, коли висота вежі дорівнює нулю. У цьому випадку нічого не відбувається, тому функція moveTower робить порожній повернення. При обробці базового випадку важливо пам'ятати, що простий повернення з moveTower - це те, що в підсумку дозволяє функції moveDisk бути викликаною.
Функція moveDisk. показана в лістингу 2. дуже проста. Все, що вона робить, - це друкує, що диск був пересунутий з одного стрижня на інший. Якщо ви наберете і запустіть програму moveTower. то побачите, як вона напише вам дуже ефективне рішення головоломки.
Програма в ActiveCode 1 містить повне рішення для задачі з трьома дисками.
Run Save Load Show in Codelens
Рекурсивне рішення задачі про Ханойські вежі. (Hanoi)
Тепер, коли ви можете бачити код і для moveTower. і для moveDisk. то можете задатися питанням: чому у нас немає структури даних, яка б явно відстежувала, який диск на якому стрижні знаходиться. Ось підказка: якщо ви будете явно відстежувати диски, то вам, можливо, доведеться використовувати три об'єкти Stack - по одному для кожного стержня. Відповідь в ж те, що Python надає в наше розпорядження стеки неявно і коли нам це потрібно.