Green filin s blog розважимося з Ейфелевої вежею
- Що таке: велика, як Ейфелева вежа, а не важить ні грама?
- Тінь від Ейфелевої вежі.
(Жартівливе запитання)
Коли я попався на цю стару штуку я подумав: "Чорт, чорт! Невже тінь від вежі дійсно нічого не важить?"
Формально, воно, звичайно так. Неможливо зважити тінь. Однак, якщо б ми "поклали" тінь на надточні ваги, що б ми отримали в результаті? Хитнулася б стрілка вагів? Можливо.
Мабуть, варто почати з того, що всі предмети освітлені сонцем відчувають на собі тиск сонячного світла. Значить, в тому місці, куди сонячне світло не потрапляє, тиск він не робить. Тобто якби на одну чашу терезів ми "поклали" б тінь від вежі, а на іншу таку-ж (природно освітлену сонцем) не «поклали", то стрілка повинна була б зрушити в сторону освітленій чаші, кажучи про те, що тінь "важить "мінус скільки-то. Отже, скільки ж?
Максвелл обчислив, а Лебедєв підтвердив. що на землі тиск сонячного світла одно всього лише 4,7 * 10 -6 Н / м 2. але ця величина справедлива для світла падаючого перпендикулярно на ідеально відбивну поверхню.
Якщо ж сонце знаходиться на висоті α (від 0 ° - у горизонту до 90 ° - в зеніті), то силу діючу в напрямку нормалі (власне силу тиску на ваги) ми легко обчислимо за формулою: Fn = F * sin (α)
Отже, для цього часу (і місця) легко дізнатися положення сонця над горизонтом за допомогою Excel-калькулятора (насправді можна було скористатися online-калькулятором. Але він не враховує перехід на літній час, тому для нього ви повинні будете зробити коригування часу на годину тому).
Ввівши координати (Вікіпедія дає нам такі дані: 48 ° 51'29''с.ш. / 2 ° 17'40''в.д. Або в дрібних градусах 48.858056 ° с.ш. / 2.294444 ° В.Д.) і часом ми отримаємо:
True (Celestial) Altitude of sun
Apparent (Refracted) Altitude of sun
Де Sun's Azimuth цей напрям на сонце (величина показує кут відхилення від напрямку на південь і, так як вона негативна, то це відхилення в бік Сходу, тобто якщо в цей час стати обличчям на північ, то сонце буде світити в попу, приємно обігріваючи праве вухо).
А Altitude of sun це якраз і є висота сонця над горизонтом. Причому True (Celestial) Altitude - дійсна, а Apparent (Refracted) Altitude здається висота, яка відрізняється від дійсної за рахунок того, що промені світла трохи переломлюються при вході в атмосферу. Незважаючи на те, що різниця невелика, краще буде взяти уявну висоту.
Отже, кут відомий: +55,75011692 °
Залишилося обчислити площу тіні Ейфелевої вежі. Як це зробити? Спеціально для цього я скачав її тривимірну модель. Можливо, точності цієї моделі недостатньо, але в разі крайньої необхідності можна буде створити або знайти більш точну модель. Поки ж обмежимося цієї.
Очистивши сцену від непотрібних декорацій я отримав цілком пристойний результат:

Далі, спозіціоніруем вежу щодо сторін світла так, як вона встановлена в реальності:

Тепер додамо паралельний джерело світла з потрібними координатами (висота і азимут) і отримаємо. Отримаємо. Правильно! Тінь від башти:

Поки нам немає ніякої користі від такої картинки, однак шляхом невеликих маніпуляцій (приховуємо саму вежу, робимо площину білої і включаємо ортогональную проекцію - вид зверху) ми можемо отримати те, що нам дійсно може стати в нагоді:

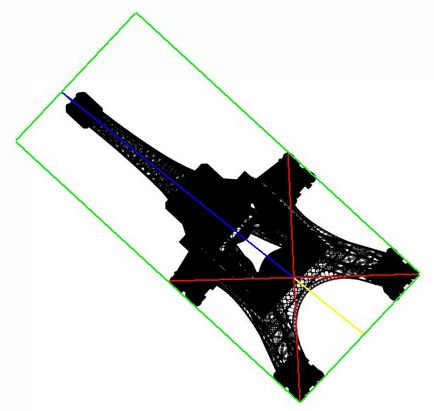
Тепер використовуючи цей малюнок нескладно підрахувати який відсоток площі зеленого прямокутника займає тінь від вежі на малюнку (назвемо цей коефіцієнт sh). А зрозумівши реальну площу такого ж прямокутника у справжньої вежі, ми шляхом множення на коефіцієнт, дізнаємося реальну площу, яку займає тінь.
Отже, нескладна програма, яка вважає чорні точки видала коефіцієнт sh = 0,38579 (природно, я використовував картинку з великою роздільною здатністю, ніж викладаю в web).
Тепер про реальну площі прямокутника. Згідно розмірами вежі ширина меншої сторони прямокутника буде дорівнює 124,9 м. (Ширина підстави вежі). І, якщо вже так вийшло, що вежа майже "стоїть обличчям" до сонця, то для спрощення будемо вважати що велика сторона прямокутника дорівнює сумі довжин синього і жовтого відрізків (там дійсно не дуже великий кут відхилення від сторони і похибка буде невелика). Довжина жовтого відрізка дорівнює половині ширини підстави вежі, а довжина синього обчислюється за формулою: x = H * ctg α
Де H - висота вежі, α - висота сонця над горизонтом.
Отримуємо, що x = 221,28 м
Значить, площа прямокутника 221,28 * 124,9 = 27637,87 м 2
Тепер застосуємо коефіцієнт sh і отримаємо, що площа тіні:
27637,87 м 2 * 0,38579 = 10662,41 м 2
Тепер, коли ми знаємо висоту сонця, по формулі Fn = F * sin (α) порахуємо силу діючу на кожен метр:
4,7 * 10 -6 Н / м 2 * sin (+55,75011692 °) = 3,88 * 10 -6 Н / м 2
І помножимо на площу тіні:
10662,41 * 3,88 * 10 -6 = 41,37 * 10 -3 Н / м 2
Що одно силі з якою вантаж масою 4,22 грама тисне на площину.
Так, що жартівник з епіграфа до цього посту сильно помилявся. Тінь від башти "важить" мінус чотири грами!
P.S. Пост писався виключно заради розваги, так що в ньому, природно, можуть бути помилки або неточності. Якщо ви знайдете такі пишіть, буду радий. До речі, ніхто не знає кращого методу обчислення площі тіні вежі?