Формула сили тяги в фізиці
У тому випадку, якщо тіло при переміщенні має прискорення, то на нього крім всіх інших обов'язково діє деяка сила, яка є силою тяги в даний момент часу. Насправді, якщо тіло рухається прямолінійно і з постійною швидкістю, то сила тяги також діє, так як тіло повинно долати сили опору. Зазвичай силу тяги знаходять, розглядаючи сили, що діють на тіло, знаходячи рівнодіюча і застосовуючи другий закон Ньютона. Жорстко певної формули для сили тяги не існує.
Не слід вважати, що сила тяги, наприклад, транспортного засобу діє з боку двигуна, так як внутрішні сили не можуть змінювати швидкість системи як єдиного цілого, що входило б в суперечність з законом збереження імпульсу. Однак слід зазначити, що для отримання у сили тертя спокою необхідного напрямку, мотор обертає колеса, колеса «чіпляються за дорогу» і породжується сила тяги. Теоретично було б можливо не використовувати поняття «сила тяги», а говорити про силу тертя спокою або силі реакції повітря. Але зручніше зовнішні сили, які діють на транспорт ділити на дві частини, при цьому одні сили називати силами тяги, а інші - силами опору. Це робиться для того, щоб рівняння руху не втратили свій універсальний вид і корисна механічна потужність (P) мала просте вираження:
Визначення і формула сили тяги
Виходячи з формули (1) силу тяги можна визначити через корисну потужність, і швидкість транспортного засобу (v):
Для автомобіля, що піднімається в гору, яка має ухил, маса автомобіля m сила тяги (FT) увійде в рівняння:
де a - прискорення, з яким рухається автомобіль.
Одиниці виміру сили тяги
Основною одиницею виміру сили в системі СІ є: [FT] = Н
Приклади розв'язання задач
Завдання. На автомобіль має масу 1 т при його русі по горизонтальній поверхні, діє сила тертя, яка дорівнює = 0,1 від сили тяжіння. Якою буде сила тяги, якщо автомобіль рухається з прискоренням 2 м / с?
Рішення. Зробимо малюнок.
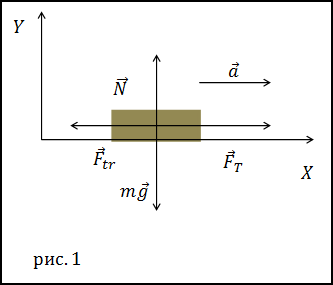
В якості основи для вирішення задачі використовуємо другий закон Ньютона:
Спроектуємо рівняння (1.1) на осі X і Y:
За умовою завдання:
Підставами праву частину виразу (1.4) замість сили тертя в (1.2), отримаємо:
Переведемо масу в систему СІ m = 1т = 10 3 кг, проведемо обчислення:
Завдання. На гладкій горизонтальній поверхні лежить дошка масою M. На дошці знаходиться тіло маси m. Коефіцієнт тертя тіла об дошку дорівнює. До дошки прикладена сила горизонтальна сила тяги, яка залежить від часу як: F = At (де A = const). В який момент часу дошка почне вислизати з-під тіла?
Рішення. Зробимо малюнок.
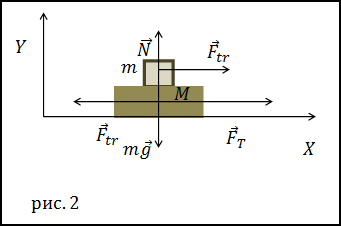
Для вирішення завдання нам будуть потрібні проекції сил на осіX і Y, які відмінні від нуля. Для тіла маси m:
Для тіла маси M:
Позначимо момент часу, в який дошка почне вислизати з-під тіла t0. тоді