Формалізація логічних висловлювань
При роботі з висловлюваннями ми відволікаємося від їх змила, нас цікавить тільки їх істинність або хибність. Кожне висловлювання - це оповідний твердження природної мови. Незважаючи на те, що природна мова набагато багатша висловлювань алгебри логіки, в наступній таблиці наведемо один із способів формалізації складних висловлювань, тобто побудови формул алгебри логіки.
Розглянемо приклади побудови формул, за умови що а- «погода ясна», b- «погода дощова», с- «вітряна погода».
Послуги спілок та частки природної мови
Операції алгебри висловлювань
погода ясна і дощова
ясна або дощова погода
буде вітряно, або дощитиме

Невірно, що погода ясна
«А» достатня умова для «б»
ясна погода є достатньою умовою дощової погоди
Якщо погода ясна, то буде дощ
«А» необхідна умова для «б»
ясна погода є необхідною умовою дощової погоди
«А» тоді і тільки тоді, коли «б»
ясна погода буває тоді і тільки тоді, коли йде дощ
погода буде ясною або дощовою, або ясна погода
або «а», або «б», але не обидва
Або сьогодні погода буде ясною, або дощовою, але не ясною з дощем
При формалізації висловлювань природної мови можна використовувати наступний підхід. Нехай дано логічне висловлювання (складене).
Виділити з складного висловлювання прості висловлювання і позначити їх латинськими літерами.
Побудувати дерево синтаксичного розбору. в якому кожній вершині відповідає логічна зв'язка (операція), а кінцевим вершин - прості висловлювання.
Записати логічну формулу шляхом обходу дерева з урахуванням структури дерева і старшинства логічних операцій.
Розглянемо логічне висловлювання:
«Неправильно, що йде дощ або вітряно і холодно»
виділяємо прості висловлювання і замінюємо їх буквами:
На першому етапі потрібно вибрати кореневу вершину.
У нашому випадку кореневої вершиною буде граматична зв'язка - "Невірно".
На другому етапі побудови дерева потрібно зрозуміти, скільки і які букви і / або граматичні зв'язки будуть перебувати на наступному рівні.
У нашому випадку буде тільки одна граматична зв'язка - «Або».
Важливо зауважити, що якщо вершиною (будь-який, не обов'язково кореневої) є «Заперечення» ( «Невірно»), то з неї може виходити тільки вона гілка.
Далі, на третьому етапі, потрібно вибрати вершину, по якій будемо продовжувати побудову дерева.
У нашому випадку вона одна, тому ми повторюємо етап номер 2 і переходимо до наступного рівня дерева: третього.
Вибираємо просте висловлювання (букву) - «А» і одну граматичну зв'язку - «і».
Повертаємося до етапу номер 3 і вибираємо вершину - "і".
Важливо запам'ятати два правила:
Завжди потрібно рухатися по дереву зверху вниз і зліва направо.
Дерево ніколи не може закінчуватися вершинами з граматичними зв'язками (операціями).
Повертаємося до 2 етапу, вибираємо прості висловлювання (літери) В і С. Дерево побудовано.
На рис. 1 представлено дерево для висловлювання: «Невірно, А або B і C».
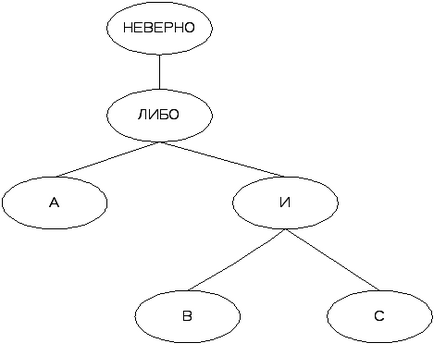
Мал. 1. Побудоване дерево для висловлювання «Невірно, А або B і C»
Замінимо граматичні зв'язки операціями над висловлюваннями (Рис.2).
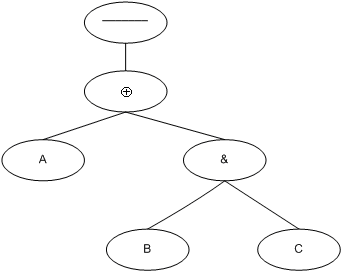
На підставі побудованого дерева ми можемо записати наше логічне висловлювання: «Невірно, йде дощ або вітряно і холодно» на мові формальної логіки: