Елементи диференціальної геометрії природна параметризація - рішення задач, контрольних

ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОЇ ГЕОМЕТРИИ Природна параметризация

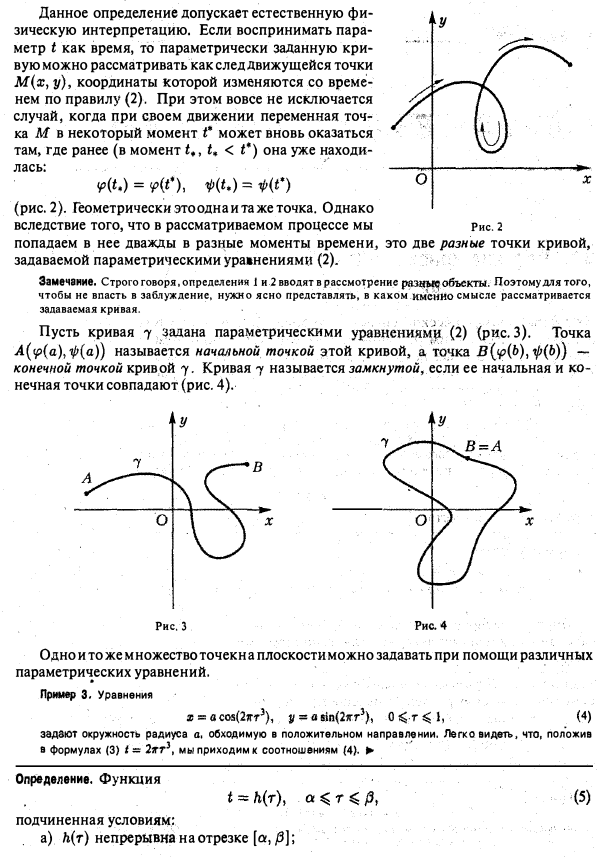
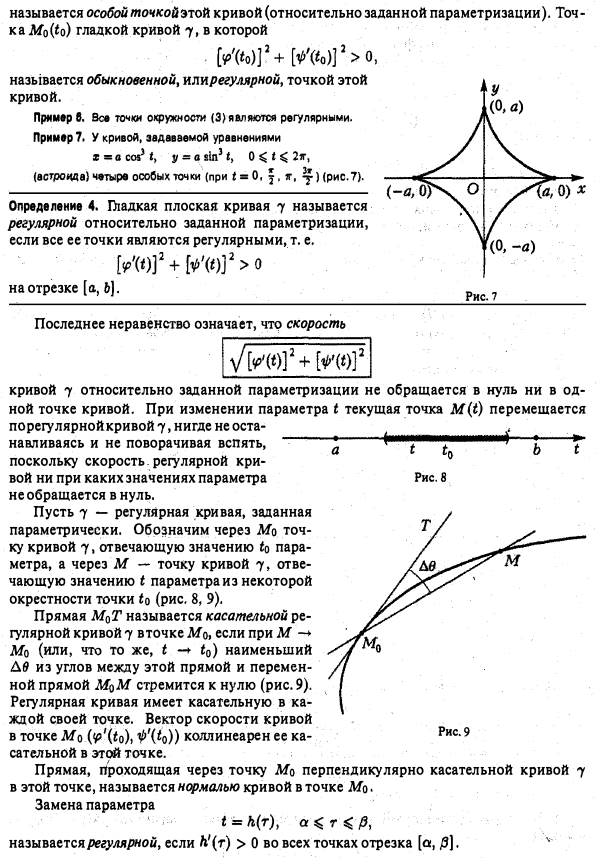
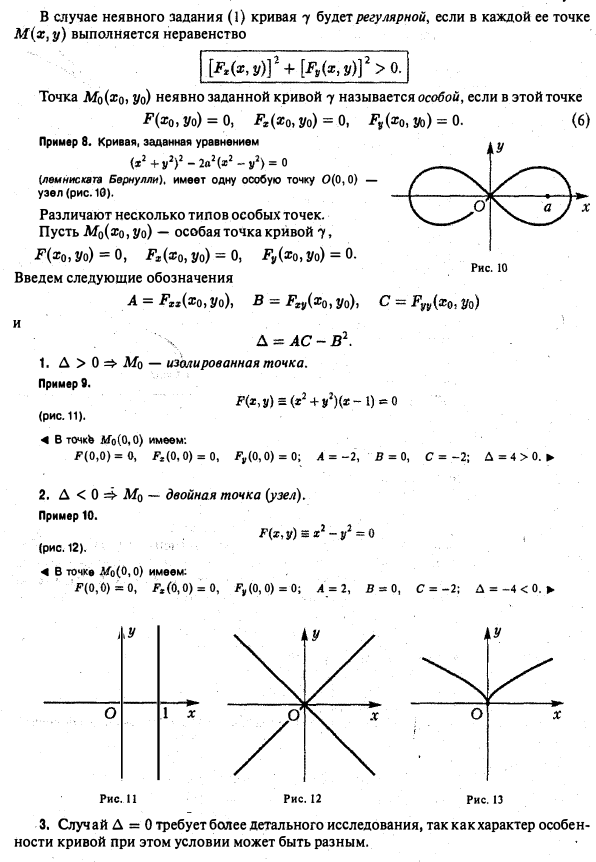
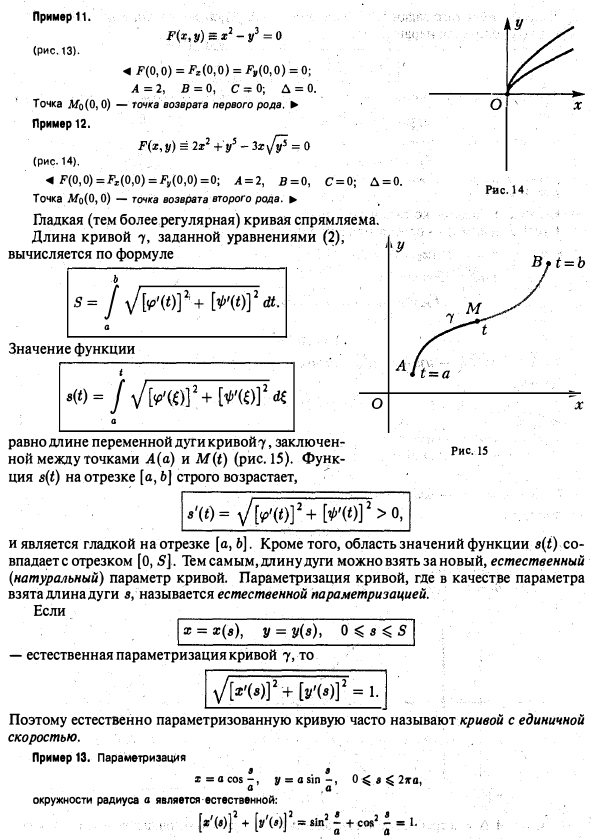
Наочний геометричний об'їсть - плоска крива - припливних визначеннях приводить до декількох різних, хоча і близьким поняттям. Плоску криву можна розуміти і як деякий безліч точок на площині і як безліч точок площині разом з черговістю їх проходження - орієнтацією. Наведемо два найбільш поширених підходу до визначення того, що представля ет собою плоска крива. Нехай на площині введена прямокутна декартова система координат Оху. Визначення 1 (неявний спосіб завдання). Плоскої кривої називається безліч 7 точок М площини, координати х і у яких при підстановці в рівняння ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОЇ ГЕОМЕТРИИ Плоскі криві. Способи завдання. Природна параметризация звертають його в тотожність. Приклад 1 Рівняння. задає коло радіуса а з центром в точці 0 (0,0) 3]; в) область значення функції h (r) - відрізок [а, Ь], називається безперервної заміною параметра кривої 7 (рис. 5). ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОЇ ГЕОМЕТРИИ Плоскі криві. Способи завдання. Природна параметризация Замінюючи в формулах (2) параметр t на функцію Л (т), отримуємо рівняння - іншу параметризацію кривої 7. Будь-яку криву можна параметризрвані багатьма різними способами. Визначення 3. Плоска крива 7 називається п-гладкою щодо параметризації якщо функції) належить класу. Якщо порядок п гладкості функцій несуттєвий, то говорять просто про гладкою кривою. Приклад 4. Крива задана рівняннями є 3-гладкою (рис. В а). Приклад S. Крива 7, задана рівняннями є 2-гладкою. Однак множин про точок на площині, що описується цими рівняннями, має • точці О (при t) особливість - злам (ріс.вб). Це означає, що гладкість функцій. задають криву, не забезпечує плавного її зміни. Відзначимо, що похідні цих функцій при tодновременно звертаються а нуль. Т'чка Мо гладкої кривої у, що відповідає значенню t0 параметра, М0 в якій називається особливою точкою цієї кривої (щодо заданої параметризації). Точка Мо (* о) гладкої кривої 7, в якій називається звичайної, ншрегулярной, точкою цієї кривої. Приклад в. Всі точки кола (3) є регулярними. Приклад 7. У кривої, що задається рівняннями (астроїда) чотири особливих точки (при t ж 0, | Остання нерівність означає, що швидкість кривої 7 щодо заданої параметризації не звертається до нуль ні в одній точці кривої. При зміні параметра t поточна точка M ( t) переміщається порегулярной кривої 7, ніде не оста- навліваясь і не повертаючи назад, оскільки швидкість регулярної кривої ні при яких значеннях параметра не звертається до нуль. Нехай 7 - регулярна крива, задана параметрично. Позначимо через Мо точку кривої 7, що відповідає знач нию £ про параметра, а через М - точку кривої 7, що відповідає значенню t параметра з деякою околиці точки to (рис. 8, 9). Пряма М0Т називається дотичній регулярної кривої 7 вточке Мо, якщо при (або, що те ж,) найменший Д0 з кутів між цією прямою і змінної прямої MqM прагне до нуля (рис. 9). Регулярна крива має дотичну в кожній своїй точці. Вектор швидкості кривої в точці Мо коллінеарен її ка- сательной в цій точці. Пряма, що проходить через точку Мо перпендикулярно дотичній кривій 7 в цій точці, називається нормаллю кривої вточ е Мо. Заміна параметра називається регулярною у якщо Л '(т у всіх точках відрізка [а, / 3]. У випадку неявного завдання (1) крива 7 буде регулярною, якщо в кожній її точці М (х, у) виконується нерівність Точка Мо (жо > Уо) неявно заданої кривої 7 називається особливою, якщо в цій точці Приклад 8. Крива, задана рівнянням (леммісюга Бернулт), має одну особливу точку 0 (0,0) - вузол (рис.10). Розрізняють декілька типів особливих точок. нехай М0 (хо, уо) - особлива точка кривої 7, Введемо наступні позначення повернення першого роду. Приклад 12. (рис. 14). - точка повернення другого роду. Гл дкая (тим більше регулярна) крива спрямляема. Довжина кривої 7, заданої рівняннями (2), обчислюється за формулою Значення функції дорівнює довжині змінної дуги крівой7, укладеної між точками (рис. 15). Функція на відрізку [а, 6) строго зростає, приклад 11. ЕЛЕМЕНТИ ДИФЕРЕНЦІАЛЬНОЇ ГЕОМЕТРИИ Плоскі криві. Способи завдання. Природна параметризация і є гладкою на відрізку [а, 6]. Крім того, область значень s (t) збігається з відрізком [0, 5]. Тим самим, довжину дуги можна взяти за новий, природний (натуральний) параметр кривої. Параметризація кривої, де в якості параметра взята довжина дуги з, називається природною параметризацією. Якщо природна параметризація кривої, то Тому природно параметризрвані криву часто називають кривою з одиничною швидкістю. Приклад 13. Параметризація окружності радіусі а є природною: