Екстремуми, найбільші і найменші значення функцій

19. Локальний екстремум функції. Необхідна умова існування екстремуму

Кажуть, що функція має вовнутреннейточке областіDлокальний максимум (мінімум), якщо існує така окрестностьточкі

, для кожної точкиякої виконується нерівність

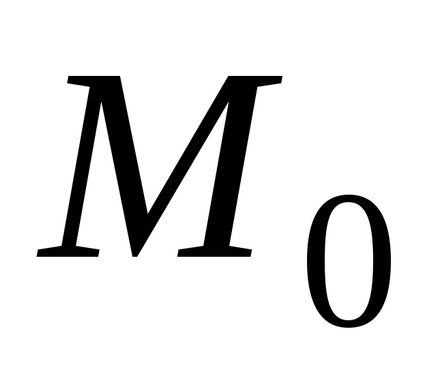
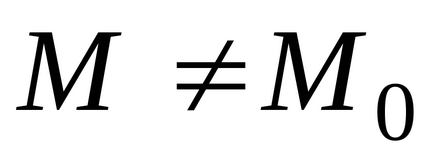
Якщо функція має в точці

локальний максимум чи локальний мінімум, то кажуть, що вона має в цій точкелокальний екстремум (або просто екстремум).

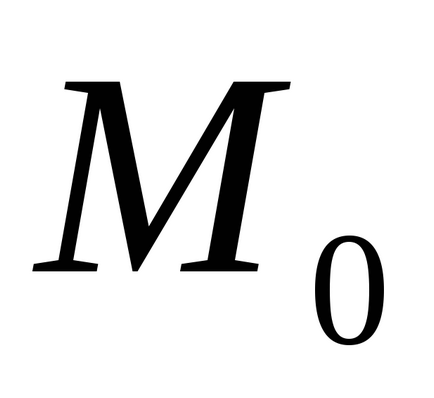
Теорема (необхідна умова існування екстремуму). Якщо дифференцируемая функціядостігает екстремуму в точці, то кожна приватна похідна першого порядку від функції

в цій точці звертається в нуль.

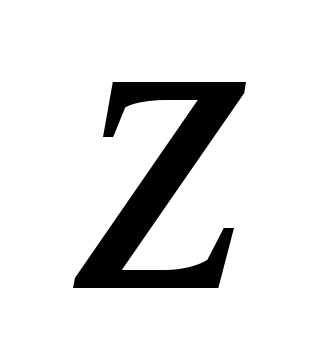
Точки, в яких всі приватні похідні першого порядку звертаються в нуль, називаються стаціонарними точками функції. Координати цих точок можна знайти, вирішивши систему з

рівнянь

.

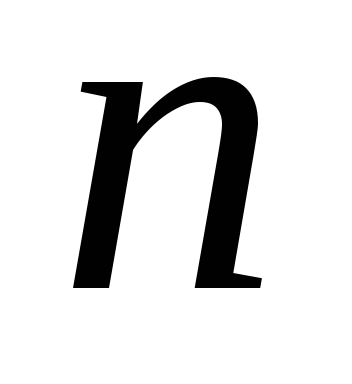
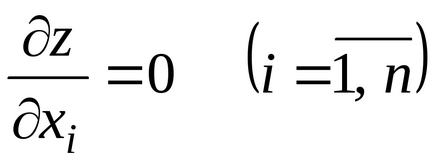
Необхідна умова існування екстремуму в разі диференціюється коротко можна сформулювати і так:

.

Зустрічаються випадки, коли в окремих точках деякі приватні похідні мають нескінченні значення або не існує (в той час як інші рівні нулю). Такі точки називаються критичними точками функції. Ці точки теж потрібно розглядати як «підозрілих» на екстремум, як і стаціонарні.

У випадку функції двох змінних необхідна умова екстремуму, а саме рівність нулю приватних похідних (диференціала) в точці екстремуму, має геометричну інтерпретацію: дотична площину до поверхні

в точці екстремуму повинна бути паралельна площині.

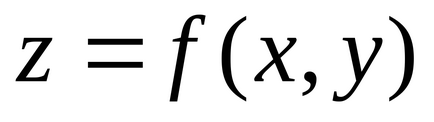
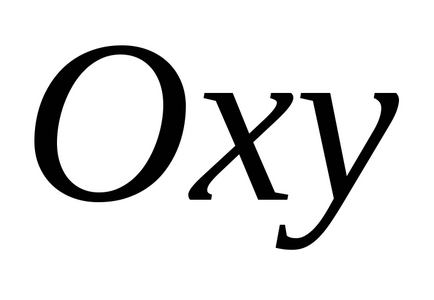
20. Достатні умови існування екстремуму

Виконання в деякій точці необхідна умова існування екстремуму зовсім не гарантує наявності там екстремуму. Як приклад можна взяти диференційовану всюди функцію

. Обидві її приватні похідні і сама функція звертаються в нуль в точці. Однак в будь-який околиці цієї точки є як позитивні (великі), Так і негативні (менші) Значення цієї функції. Отже, в цій точці, за визначенням, екстремуму не спостерігається. Тому необхідно знати достатні умови, при яких точка, підозріла на екстремум, є точкою екстремуму досліджуваної функції.

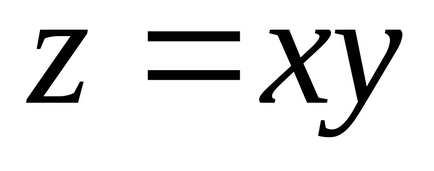
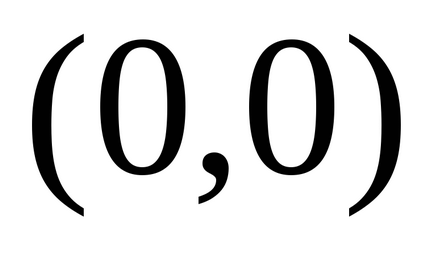
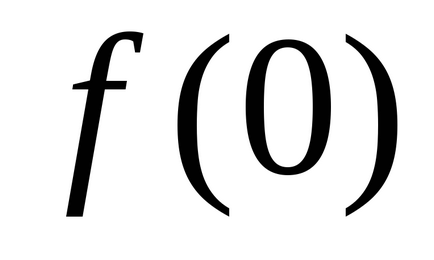
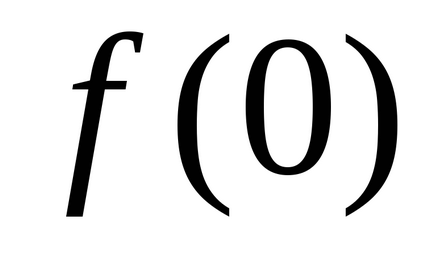
Розглянемо випадок функції двох змінних. Припустимо, що функція

визначена, неперервна і має безперервні приватні похідні до другого порядку включно в околиці деякої точки, яка є стаціонарною точкою функції, тобто задовольняє умовам

,

.

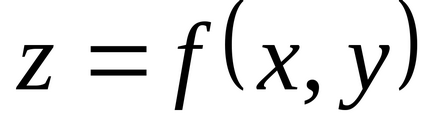
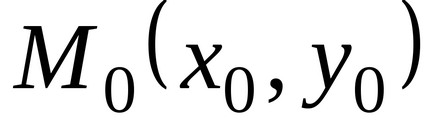
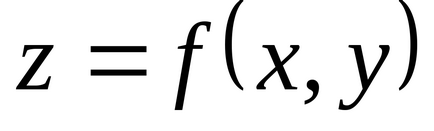
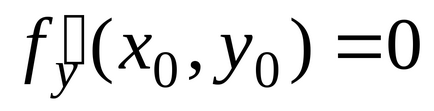
Теорема (достатні умови існування екстремуму). нехай функція

задовольняє вищенаведеним умовам, а саме: диференційована в деякому околі стаціонарної точкиі двічі диференційовна в самій точці. Тоді, якщо

, то в досліджуваній точці функція має локальний екстремум,

то екстремуму немає,

то потрібне додаткове дослідження.

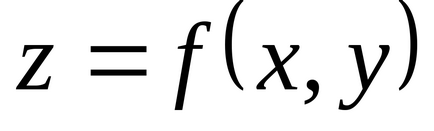
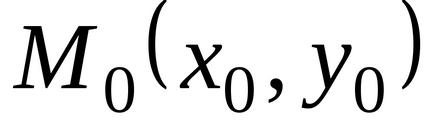
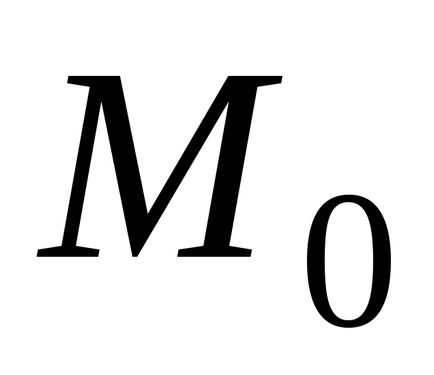
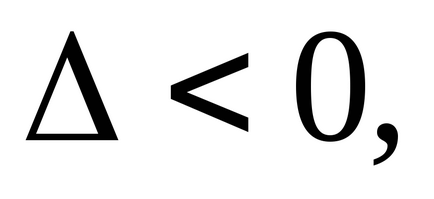
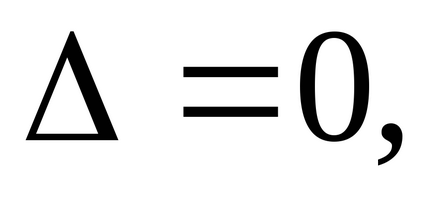
У разі якщо

то функціяв точцідосягає

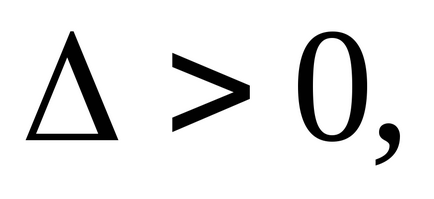
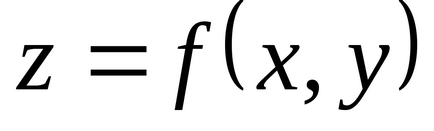
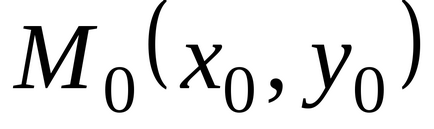
локального максимуму при

і

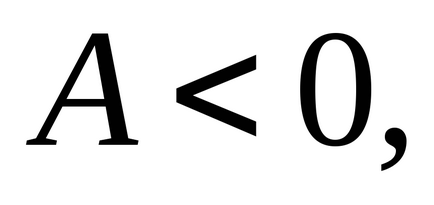
локального мінімуму при

.

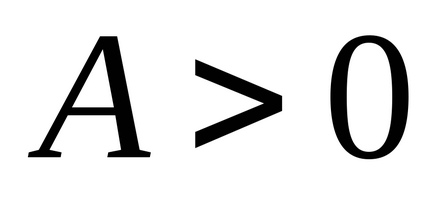
У загальному випадку, для функції достатньою умовою існування в точкелокальногомінімума (максимуму) являетсяположітельная (негативна) визначеність другого диференціала.

Іншими словами, справедливо наступне твердження.

Теорема. Якщо в точкедля функції

для будь-яких не рівних одночасно нулю

, то в цій точці функція імеетмінімум (аналогічномаксімум. якщо).

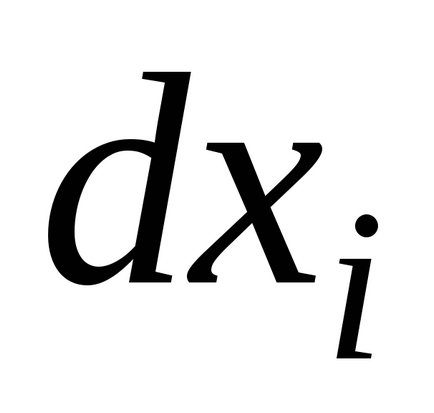
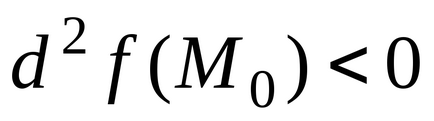
Приклад 18.Найті точки локального екстремуму функції

Рішення. Знайдемо приватні похідні функції і прирівнюємо їх до нуля:

Вирішуючи цю систему, знаходимо дві точки можливого екстремуму:

Знайдемо приватні похідні другого порядку для даної функції:

У першій стаціонарній точці, отже, іпоетому для цієї точки потрібне додаткове дослідження. значення функції

в цій точці дорівнює нулю:далі,

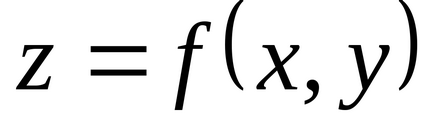
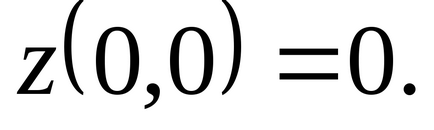
Отже, в будь-який околиці точки

функціяприймає значення як великі, так і менші, і, отже, в точціфункція, за визначенням, не має локального екстремуму.

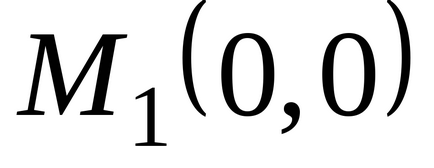
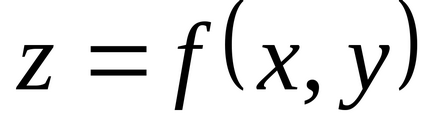
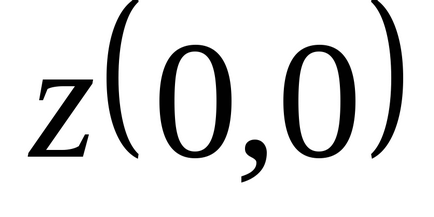
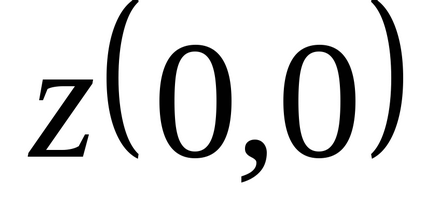
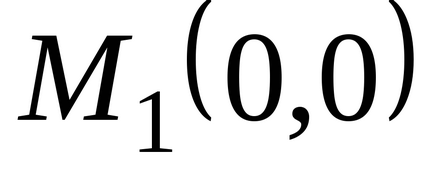
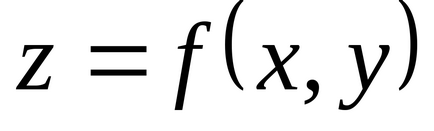
У другій стаціонарній точці

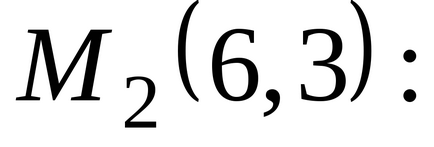
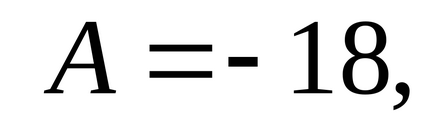
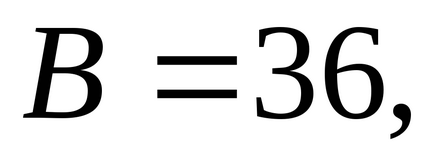
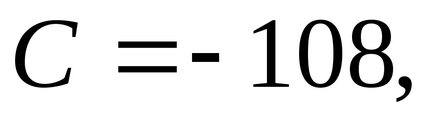
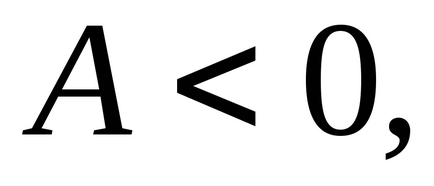
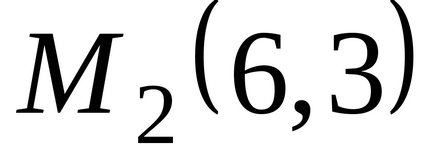
отже, Тому, так якто в точціфункція має локальний максимум:

.