Друга ознака екстремуму функції
якщо, то - точка максимуму.
Як бачите, ця ознака екстремуму функції вимагає існування похідної як мінімум до другого порядку в точці.
Знайти екстремуми функції.
Почнемо з області визначення:
Продифференцируем вихідну функцію:
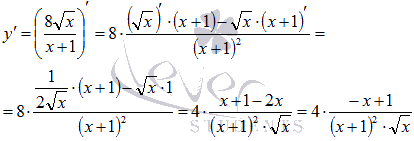
Похідна звертається в нуль при x = 1. тобто, це точка можливого екстремуму. Знаходимо другу похідну функції і обчислюємо її значення при x = 1.
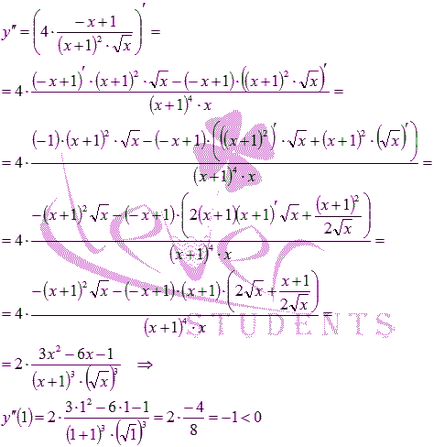
Отже, за другим достатньому умові екстремуму, x = 1 - точка максимуму. Тоді - максимум функції.
Третє достатня умова екстремуму функції.
Нехай функція y = f (x) має похідні до n -ого порядку в -окрестності точки і похідні до n + 1 -ого порядку в самій точці. Нехай і.
якщо n - парне, то - точка перегину;
якщо n - непарне, то - точка екстремуму, причому
якщо, то - точка мінімуму;
якщо, то - точка максимуму.
Знайти точки екстремуму функції.
Вихідна функція є цілою раціональною, її областю визначення є вся безліч дійсних чисел.
Похідна звертається в нуль при, отже, це точки можливого екстремуму. Скористаємося третім достатньою умовою екстремуму.
Знаходимо другу похідну і обчислюємо її значення в точках можливого екстремуму (проміжні обчислення опустимо):

Отже, - точка максимуму (для третього достатнього ознаки екстремуму маємо n = 1 і).
Для з'ясування характеру точок знаходимо третю похідну і обчислюємо її значення в цих точках:
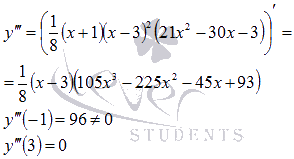
Отже, - точка перегину функції (n = 2 і).
Залишилося розібратися з точкою. Знаходимо четверту похідну і обчислюємо її значення в цій точці:
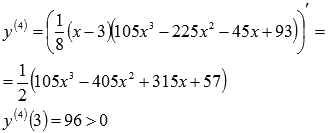
Отже, - точка мінімуму функції.
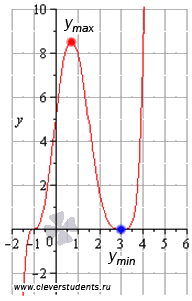
- точка максимуму, - точка мінімуму функції.
10. Екстремуми функції Визначення екстремуму
Функція y = f (x) називається зростаючою (спадною) в деякому інтервалі, якщо при x1
Якщо диференційована функція y = f (x) на відрізку [a, b] зростає (спадає), то її похідна на цьому відрізку f '(x) 0
Точка Xо називається точкою локального максимуму (мінімуму) функції f (x), якщо існує околиця точки Xо. для всіх точок якої вірно нерівність f (x) ≤ f (Xо) (f (x) ≥ f (Xо)).
Точки максимуму і мінімуму називаються точками екстремуму. а значення функції в цих точках - її екстремумами.
точки екстремуму
Необхідні умови екстремуму. Якщо точка Xо є точкою екстремуму функції f (x), то або f '(Xо) = 0, або f (Xо) не існує. Такі точки називають критичними, причому сама функція в критичній точці визначена. Екстремуми функції слід шукати серед її критичних точок.
Перше достатня умова. Нехай Xо - критична точка. Якщо f '(x) при переході через точку Xо змінює знак плюс на мінус, то в точці Xо функція має максимум, в іншому випадку - мінімум. Якщо при переході через критичну точку похідна не змінює знак, то в точці Xо екстремуму немає.
Друге достатня умова. Нехай функція f (x) має похідну f '(x) в околі точки Xо і другу похідну в самій точці Xо. Якщо f '(Xо) = 0,> 0 (<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На відрізку [a, b] функція y = f (x) може досягати найменшого або найбільшого значення або в критичних точках, або на кінцях відрізка [a, b].
Приклад 3.22. Знайти екстремуми функції f (x) = 2x 3 - 15x 2 + 36x - 14.
Рішення. Так як f '(x) = 6x 2 - 30x +36 = 6 (x -2) (x - 3), то критичні точки функції x1 = 2 і x2 = 3. Екстремуми можуть бути тільки в цих точках. Так як при переході через точку x1 = 2 похідна змінює знак плюс на мінус, то в цій точці функція має максимум. При переході через точку x2 = 3 похідна змінює знак мінус на плюс, тому в точці x2 = 3 у функції мінімум. Зрозумівши значення функції в точках x1 = 2 і x2 = 3, знайдемо екстремуми функції: максимум f (2) = 14 і мінімум f (3) = 13.