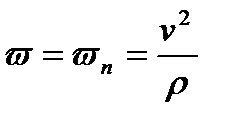1) .Прямолінейное рух. Якщо траєкторією точки є пряма лінія, то. тоді
і все прискорення точки дорівнює одному тільки дотичному прискоренню:. Так як в даному випадку швидкість змінюється тільки чисельно, то звідси робимо висновок, що дотичне прискорення характеризує зміну швидкості за чисельної величиною. 2). Рівномірний криволінійний рух. Рівномірним називається таке криволінійний рух точки, в якому чисельна величина швидкості весь час залишається незмінною:. Тоді і все прискорення точки дорівнює одному тільки нормальному прискоренню:
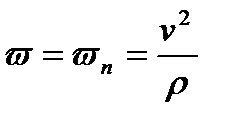
. Вектор прискорення спрямований при цьому весь час по нормалі до траєкторії точки. Так як в даному випадку прискорення з'являється тільки за рахунок зміни напрямку швидкості, то звідси робимо висновок, що нормальне прискорення характеризує зміну швидкості за напрямком. 3). Рівномірний прямолінійний рух. В цьому випадку . а значить і. Зауважимо, що єдиним рухом, в якому прискорення точки весь час дорівнює нулю, є рівномірний прямолінійний рух. 4). Равнопеременное криволінійний рух. Равнопеременное називається таке криволінійний рух точки, при якому дотичне прискорення залишається весь час величиною постійною:. Формулу представимо у вигляді Вдруге інтегруючи, знайдемо закон равнопеременное криволінійного руху точки у вигляді Якщо при криволінійному русі точки модуль швидкості зростає, то рух називається прискореним, а якщо зменшується - уповільненим. Так як зміна модуля швидкості характеризується дотичним прискоренням, то рух буде прискореним, якщо величини і мають однакові знаки. Зокрема, при равнопеременное русі, якщо в рівність і. мають однакові знаки, рух буде рівноприскореному, а якщо різні знаки - равнозамедленно. 5). Гармонійні коливання. Розглянемо прямолінійний рух точки, при якому її відстань x від початку координат Про змінюється з часом за законом. Коливання, що відбуваються за законом, відіграють велику роль в техніці. Вони називаються простими гармонійними коливаннями. Величина а, рівна найбільшому відхиленню точки від центру коливань О, називається амплітудою коливань. Проміжок часу . протягом якого точка здійснює одне повне коливання, називається періодом коливань. Визначення проекцій прискорення точки на дотичну і головну нормаль (дотичне і нормальне прискорення). Обчислимо проекції вектора a на осі М # 964; і Мn. Так як Vт = ds / dtтопроекціяускореніянакасательную (дотичне прискорення) ______________________ Воно характеризує зміну швидкості точки тільки за величиною і дорівнює першій похідній за часом від проекції швидкості точки на на- правління дотичній (від алгебраїчної швидкості точки) або другої похідної за часом від закону руху точки по траєкторії. Знайдемо тепер проекцію прискорення на головну нормаль (нормальноеускореніе). Діфференцірованіевектора T 0 неізменнойвелічіни призводить дозбільшення його модуля в da / dt раз, де в даному випадку a - кут суміжності. Замінюючи ___________________ і ____________ отримуємо _________________ Нормальне прискорення характеризує зміну швидкості тільки по напрямку. Нормальне прискорення дорівнює відношенню квадрата швидкості до радіуса кривизни. Нормальне прискорення завжди спрямоване по головній нормалі в сторону угнутості траєкторії (до центру кривизни). Розкладаючи прискорення на складові по природним осях, отримаємо __________________ Модуль прискорення _________________ Направленіеускореніяопределімпоформуле _______________ де μ - кут між повним прискоренням a і нормаллю. Окремі випадки руху точки:
# 945; n = 0, # 945; # 964; = 0 - прямолінійний рівномірний рух, V = const;
# 945; n = 0, # 945; # 964; ≠ 0 - прямолінійний нерівномірний рух;
# 945; n ≠ 0, # 945; # 964; = 0 - криволінійне нерівномірний рух, V = const;
# 945; n ≠ 0, # 945; # 964; ≠ 0 - криволінійне рівномірний рух.
Схожі статті