Дифракція електромагнітних хвиль, контент-платформа
33. Дифракція електромагнітних хвиль.
Геометрична оптика вірна тільки тоді, коли довжина хвилі може вважатися нескінченно малої. Якщо це не так, то будуть спостерігатися відхилення від законів геометричної оптики-явища дифракції. Для розрахунку картини дифракції був запропонований принцип Гюйгенса-Френеля, згідно з яким кожна точка хвильового фронту є джерелом вторинних хвиль, а дифрагованим хвиля виходить в результаті їх інтерференції.
Математичне формулювання принципу Гюйгенса-Френеля була дана Кирхгофом. Ми будемо розглядати дифракцию скалярних монохроматичних хвиль. У разі дифракції електромагнітних хвиль такої скалярною величиною може бути, наприклад, - компонента вектора електричного поля в хвилі. Така скалярная теорія є приблизною, але, тим не менш, вона цілком задовільно описує дифракцію світла при малому відхиленні від законів геометричної оптики, що дуже важливо для задач інструментальної оптики.
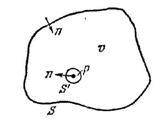
(2). де береться внутрішня нормаль до поверхні. Якщо функція також задовольняє рівняння (1), то ліва частина (2) буде дорівнює нулю. В якості опції візьмемо сферичну хвилю -, де - відстань, відраховані від точки. Ця функція має особливість в точці, тому оточимо її сферою і застосуємо формулу Гріна для обсягу, укладеного між і. . Інтегрування по сфері дає (при прагненні радіусу сфери до нуля). Тоді остаточно отримуємо: (3) це і є формула Гельмгольца-Кірхгофа. Таким чином, для того, щоб дізнатися поле в деякій точці обсягу, нам необхідно знати розподіл поля і його нормальної похідної на поверхні цього обсягу.
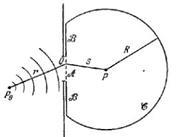
Розглянемо дифракцію монохроматичної хвилі від точкового джерела на отворі в екрані. Для знаходження поля в точці нам необхідно обчислити інтеграл (3) по всій замкнутій поверхні .Але інтеграл по сфері можна вважати рівним нулю при. Це вірно, якщо припустити, що випромінювання не існувало нескінченно довго, і не встигло дійти до кордонів сфери. Тобто ми трохи відходимо від умови монохроматичности (монохроматичне випромінювання існує завжди), але фізично все вірно. Тоді залишається інтеграл по області отвори. Врахуємо, що, тоді з (3) отримаємо (4). Тепер, якщо в якості поверхні вибрати сферичний хвильовий фронт джерела, то ми отримаємо:
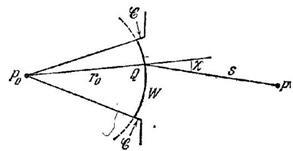
Видно, що формула (4) симетрична щодо джерела і точки. Тобто джерело тієї ж інтенсивності, поміщений в точку справив би в таку ж дію, як виробляє в точці. Це є теорема взаємності Гельмгольца.
З попередніх міркувань можна відразу ж зробити висновок про розподіл світла, дифрагованим на додаткових один одному екранах, т. Е. На екранах, у яких отвори одного точно збігаються з непрозорими частинами іншого і навпаки. Нехай - комплексні обурення, коли тільки один з екранів поміщений на шляху між джерелом і точкою спостереження. Тоді, оскільки їх можна представити у вигляді інтегралів по отворах, а отвори в додаткових екранах розташовуються так, що повністю «відкривають» весь хвильовий фронт, то
Це так званий принцип Бабині.
З принципу Бабині можна вивести наступні висновки. Якщо, то, тобто. Е. В точках, де інтенсивність при наявності одного екрану дорівнює нулю, в присутності лише одного екрану вона буде такою ж, як і під час відсутності екранів. А в точках, де за відсутності екранів, і рівні по амплітуді і відрізняються по фазі на.
Дифракція Фраунгофера і Френеля.
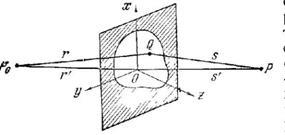
Розглянемо інтеграл (4). Коли ми інтегруємо по отвору, змінюється набагато швидше, ніж, і, крім того, якщо відстані від точок і до екрану великі, то і. Де - кут між нормаллю до екрану і прямий. Тоді (4) можна переписати в наступному вигляді: (5) (і -Відстань до точки). -початок декартової системи координат. У цій системі координат:,. Тепер ми хочемо перейти до координат і (зверніть увагу на осі координат на малюнку!), Які змінюються в площині отвору. Якщо це зробити, то отримаємо:
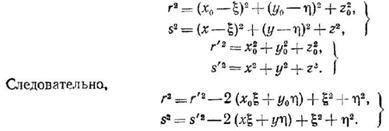
Далі, знаходимо і, розкладаючи в ряд за ступенями ,,,.
Підставивши ці значення в (5), ми отримаємо:
Тепер, якщо в ми можемо знехтувати членами порядки вище 1 по і, то ми маємо справу з дифракцією Фраунгофера. якщо ж квадратичними і більш високими членами знехтувати не можна то спостерігається дифракція Френеля. Очевидно, що наближення Фраунгофера може бути застосовано, коли точка спостереження і джерело знаходяться поблизу осі і на великій відстані від екрану. Це відповідає ситуації, коли відхилення від геометричної оптики не надто велике.
Зазвичай, для спостереження дифракції Фраунгофера використовується збирає лінза, а вся дифракційна картина виходить в фокальній площині. Це можливо, так як лінза не вносить додаткової різниці ходу між променями, котрі збираються в одну точку зображення.
Дифракція Фраунгофера на прямокутнику.
Розглянемо дифракцію світла на прямокутнику. З (6) маємо з урахуванням тільки перших двох доданків в.
А інтенсивність світла, де - інтенсивність в центрі картини.
У разі дифракції світла від протяжного некогерентного джерела, необхідно підсумувати інтенсивність від усіх точок джерела. Якщо різні точки джерела когерентні, то необхідно інтегрувати комплексниеамплітуди.
Так, наприклад, в разі дифракції світла від тонкої довгої дроту на щілини, розподіл інтенсивності має вигляд. .
Зауважимо, що формула (7) являє собою двовимірне перетворення Фур'є поля на поверхні екрану. Коли хвильовий фронт обмежений, в перетворенні Фур'є з'являються плоскі хвилі, що поширюються під різними кутами - тобто дифраговані хвилі.
37.Еффект Зеемана і Ефект Штарка.
Розглянемо Гамільтоніан атома, поміщеного в однорідне магнітне поле.
Де підсумовування проводиться по всіх електронів,-енергія взаємодії електронів з ядром і один з одним,-оператор повного електронного спина атома, -векторний потенціал поля. У разі однорідного магнітного поля він дорівнює: (2).
Розглянемо комутатор, коли векторний потенціал обраний у вигляді (2), і, таким чином, оператор узагальненого імпульсу комутує з оператором. Скориставшись цим при розкритті дужок в (1). отримаємо:
Підставивши сюди з 2 отримаємо.
-оператор повного орбітального моменту атома.
Залежно від напруженості магнітного поля, можна виділити 3 випадки розщеплення енергетичних рівнів атома:
Слабке магнітне поле, ми нехтуємо квадратичним по полю складовою; розщеплення рівнів за рахунок магнітного поля менше, ніж відстань між рівнями тонкої структури-Аномальний ефект Зеемана. Слабке поле. Як і раніше нехтуємо квадратичними складовими, але розщеплення рівнів перевершує величину тонкої структури. Ефект Пашена-Бака. При сильних полях враховується квадратичне доданок - квадратичний ефект Зеемана.
Аномальний ефект Зеемана.
В даному випадку оператором обурення є. Незбурених рівні енергії не залежать від проекції повного моменту імпульсу, тому необхідно застосовувати теорію збурень для вироджених рівнів. Розглянемо матрицю оператора обурення:, де-оператор повного моменту атома, а -невозмущенние хвильові функції.
Очевидно, що (3). Далі, необхідно обчислити (4). Ми будемо припускати, що для даного рівня має місце LS зв'язок, тобто він характеризується певними значеннями L, S, J.
Для обчислення (3) скористаємося співвідношенням а також очевидним рівністю. Так як L, S, J мають певне значення в стані, то величини,, можна замінити їх власними значеннями. Тоді отримаємо: І остаточно: Тобто матриця обурення діагональна, тому обурені рівні енергії є, де-фактор Ланде для даного рівня. Ми бачимо, що -кратноє вироджений рівень ламався й виродження повністю знялося. Відзначимо, що розщеплення може бути відсутнім і в разі, коли, наприклад, в стані.
(Прим: ще один висновок можна подивитися в Ландау, а ще краще подивитися, як це виводить Голубовський - там вектора прецессируют і все таке)
У тому випадку, коли магнітне поле дуже велике, і зєємановських розщеплення перевершує інтервали тонкої структури, формули попереднього розділу виявляються невірні. У цьому випадку енергія в магнітному полі значно перевищує спін-орбітальна взаємодія. Тому в першому наближенні ми цим взаємодією прінебрегать.
Тоді рветься зв'язок між векторами L і S і вони починають незалежно один від одного квантованим на напрямок магнітного поля, тобто має сенс не тільки величина, але і та. Тоді:.
Розглянемо атом, що знаходиться в постійному електричному полі. Так як поле має осьову симетрію, то зберігається проекція повного моменту на напрямок поля. Однак, істотна різниця в порівнянні з магнітним полем полягає в тому, що додаткова енергія залежить тільки від абсолютного значення. Тому стану з однаковим виродилися. В результаті відбувається неповне розщеплення рівня з даними на підрівні зі значеннями: -при цілому, тобто на підрівень. І при напівцілий на підрівні зі значеннями -на.
Розглянемо питання про залежність штарковского розщеплення від напруженості електричного поля. Додаткова енергія системи, яка має дипольним моментом, що знаходиться в електричному полі дорівнює. Якщо, то спостерігається лінійне явище Штарка.
Однак, на відміну від магнітного моменту, дипольний зараз не квантуется і заданий стан системи характеризується середнім значенням цього моменту. Для систем, що володіють центральної симетрією (атоми, гомоядерних молекули) середнє значення дипольного моменту дорівнює нулю. Тому для таких систем лінійний по полю ефект Штарка спостерігатися не буде.
Однак, система, вміщена в електричне поле, може набувати індукований дипольний момент, який при не дуже сильних полях пропорційний:, де -полярізуемость (зауважимо, що у молекул вона - тензор). Тоді додаткова енергія буде дорівнює.
У сильних полях, коли додаткова енергія порівнянна з відстанями між рівнями, може спостерігатися лінійне явища Штарка. Таке розщеплення спостерігається для атома водню.
Поляризуемость атома залежить від. Приблизно ця залежність має такий вигляд:. Таким чином .
Картина Штарковского розщеплення спектральної лінії визначається розщепленням комбінує рівнів і правилами відбору. Варто зазначити, що величина квадратичного Штарковского розщеплення завжди мала і складає долі.
В результаті Штарковского розширення при зіткненні з зарядженими частинками (наприклад в зірках або плазмі) відбувається зсув рівня континууму в область більш низьких енергій. Континуум починається з такого номера рівня, коли величина Штарковского розширення перевершує відстань між рівнями.