Автоморфізм - це
Автоморфізм моделі - ізоморфізм. відображає модель на себе.
Сукупність усіх автоморфізмів деякої моделі з операцією композиції і тотожним відображенням як нейтрального елемента утворює групу.
Група автоморфізмів моделі позначається.
- Автоморфізм безлічі є перестановка елементів цієї множини
- Автоморфізм групи - ізоморфізм групи на себе.
Автоморфізм називається внутрішнім, якщо існує такий елемент, що, а в іншому випадку зовнішнім. Безліч всіх внутрішніх автоморфізмів групи G є підгрупа групи всіх автоморфізмів, причому. [1]
Безліч автоморфізмів групи Лі також утворює групу Лі. [2]
автоморфізм груп
Група автоморфізмів групи позначається. Відображення автоморфизм групи, такі автоморфізм групи називаються внутрішніми, безліч внутрішніх автоморфізмів позначається. Оскільки і, то - нормальна підгрупа в. Фактор-група називається групою зовнішніх автоморфізмів групи, а її елементи - зовнішніми автоморфізм. Відображення визначає гомоморфізм, ядро якого є центр групи, так що. Всі нормальні підгрупи інваріантні під дією внутрішніх автоморфізмів. Підгрупи, інваріантні під дією всіх автоморфізмів групи, називаються характеристичними.
Будь-яка група, що збігається зі своєю групою автоморфізмів, називається досконалою. Досконалими є все симетричні групи при. Розширення групи, за допомогою групи автоморфізмів, називається голоморфа.
- , *
- - поле характеристики більшою 2.
- Група автоморфізмів безлічі всіх комплексних коренів ступенів * з одиниці є група p -адіческіх чисел по складанню.
- Група зовнішніх автоморфізмів вільної групи кінцевого рангу породжується перетвореннями Нільсена елементів базису
автоморфізм кілець
автоморфізм полів
автоморфізм графів
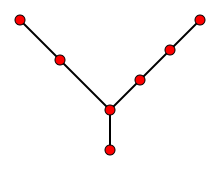
Найменша асиметричне дерево
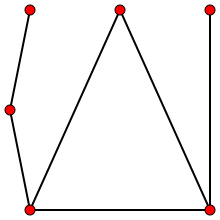
Найменший асиметричний граф
Автоморфізм графа є відображення безлічі вершин на себе, що зберігає суміжність. [3] Безліч таких автоморфізмів утворює вершину групу графа або просто групу графа. Група підстановок на безлічі ребер називається реберної групою графа. яка тісно пов'язана з вершинної:
Реброва і верхова групи графа ізоморфні тоді і тільки тоді, коли є не більше однієї ізольованої вершини. і немає компонент зв'язності складаються з єдиного ребра. [4]
Граф, для якого єдиний можливий автоморфизм це тотожне відображення, називається асиметричним. Найменша асиметричне дерево має сім вершин, а найменший асиметричний граф шість вершин і стільки ж ребер.
Для будь-якої кінцевої групи знайдеться такий кінцевий неорієнтований граф, що його група автоморфізмів ізоморфна даної. [5] Результат отриманий Р. Фрухт, в основі докази - перетворення кольорового графа групи. узагальнення графа Келі. [6] [7]
Примітки
література
Дивитися що таке "Автоморфізм" в інших словниках:
автоморфизм - автоморфизм ... Орфографічний словник-довідник
автоморфизм<–> - мат. поняття, що виражає властивість однаковості будови будь-яких сукупностей (зборів) елементів, абсолютно байдуже до природи цих елементів; якщо між двома настроями елементів однієї і тієї ж сукупності має місце ізоморфізм ... Словник іншомовних слів української мови
Автоморфізм - ізоморфізм (изоморфное відображення) недо рій системи об'єктів на себе. Сукупність усіх А. довільній алгебраїч. системи є групою; вивчення цієї групи служить важливим і зручним знаряддям вивчення властивостей самої системи (див. алгебраїчних ... ... Математична енциклопедія
Автоморфізм - (матем.) См. В статті Ізоморфізм (в математиці) ... Велика радянська енциклопедія
автоморфизм - автоморфизм, автоморфізм, автоморфізм, автоморфізмів, автоморфізм, автоморфізм, автоморфизм, автоморфізм, автоморфизмом, автоморфізм, автоморфізм, автоморфізм (Джерело: «Повна акцентуйовані парадигма по А. А. Залізняку») ... Форми слів
автоморфизм - автоморф вим, а ... український орфографічний словник