Амплітуда коливань, теорія і онлайн калькулятори
Рухи, що повторюються або процеси називають коливаннями.
Залежно від природи коливання можуть бути механічними, електромагнітними, звуковими та ін. Різні види коливань описують за допомогою однакових рівнянь і при цьому використовують однакові характеристики.
Коливання називають вільними (йди власними), якщо вони відбуваються за рахунок енергії, яка отримана колебательной системою один раз і надалі зовнішніх впливів на цю систему немає.
Найпростішим видом коливань є гармонійні коливання.
Гармонійними коливаннями називають такі коливання, при яких коливається величина змінюється в часі за законом синуса або косинуса ..
Нехай відбуваються гармонійні коливання деякого параметра $ s $, тоді ці коливання можна описати за допомогою наступного рівняння:
де $ A = s_ $ - амплітуда коливань; $ _0 $ - циклічна (кругова) частота коливань; $ \ Varphi $ - початкова фаза коливань (фаза при $ t = 0 $); $ (_ 0t + \ varphi) $ - фаза коливань.
Амплітудою називають максимальною значення величини, коливання якої розглядають. Так як косинус (як і синус) змінюється в межах від одиниці до мінус одиниці, то величина $ s $ знаходиться в межах $ -A \ le s \ le $ + A.
Метод обертового вектора амплітуди коливань
Гармонійні коливання можна зображувати графічно (рис.1), при цьому використовують метод векторних діаграм (або метод обертового вектора амплітуди). З цією метою, з якою - то довільно обраної точки осі X, назвемо її точка O, під кутом рівним початковій фазі (кут $ \ varphi $), відкладають вектор $ \ overline $. Довжина цього вектора дорівнює амплітуді ($ A $) коливань. Якщо цей вектор приводиться в обертання з кутовою швидкістю $ _0 $, то проекція кінця цього вектора переміщується по осі X і приймає значення від $ -A $ до $ A $, при цьому закон коливається величини буде таким, як представляє рівняння (1). Виходить, що гармонійні коливання можна зобразити за допомогою проекції на деяку вісь вектора амплітуди $ \ overline $, який відкладений довільної точки цієї осі під кутом $ \ varphi $, що обертається з кутовою швидкістю $ _0 $ навколо обраної точки.
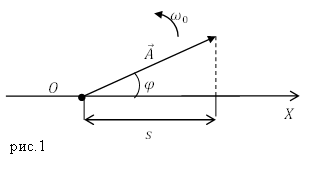
Приклади завдань з рішенням
Завдання. Матеріальна точка здійснює гармонічні коливання, які описує рівняння: $ x = 0,1_0t + \ varphi) (м) \> $. Відомо, що період коливань цієї точки дорівнює T = 5 c. Яка амплітуда швидкості ($ v_m $) і амплітуда прискорення ($ a_m $) даної точки?
Рішення. Перш за все, знайдемо циклічну частоту коливань точки, так як нам відомий період коливань:
Знаючи закон зміни координати, визначимо, як змінюється швидкість матеріальної точки:
де $ x_m = 0,1 $ за умовою задачі.
З рівняння (1.2) випливає, що амплітуда швидкості коливань точки дорівнює:
Використовуючи закон зміни швидкості, отримаємо закон зміни прискорення точки:
Із закону (1.3) випливає, що амплітуда прискорення точки дорівнює:
Завдання. До горизонтальної пружині, коефіцієнт пружності якої дорівнює $ k, $ прикріплений куля масою $ M $. Куля знаходиться на гладкому столі, за яким може переміщатися без тертя. Куля летить горизонтально і вдаряється об кулю, застряє в ньому. Швидкість кулі до удару дорівнює $ v_0 $, маса кулі $ m $, швидкість її в момент удару спрямована паралельно осі пружини. Яка амплітуда коливань кулі з кулею? Масу пружини і опір повітря не враховувати.
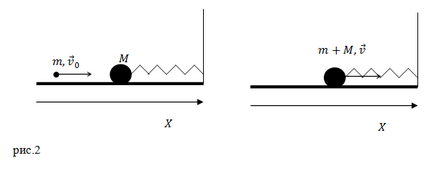
Рішення. Запишемо закон збереження імпульсу для системи куля - куля (до удару) і куля з кулею відразу після удару:
З рис.2 випливає, що вираз (2.1) можна перетворити до вигляду:
З (2.2) висловимо швидкість кулі з кулею відразу після удару:
Система куля куля, виведена зі стану рівноваги ударом кулі. Вона робить вільні гармонічні коливання. Кінетична енергія переходить в потенційну енергію стиснутої пружини. Для двох станів системи (перший стан - максимальна швидкість руху системи, друге стан максимальне стиснення пружини) відповідно до закону збереження енергії запишемо:
де $ x_m $ - амплітуда коливань кулі з кулею. Підставами величину швидкості з (2.3) в (2.4) і висловимо амплітуду: